
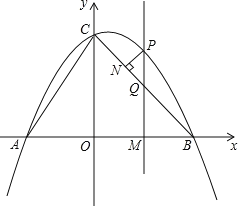
【題目】如圖,拋物線![]() 交
交![]() 軸于
軸于![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,連接
,連接![]() .點
.點![]() 是第一象限內拋物線上的一個動點,點
是第一象限內拋物線上的一個動點,點![]() 的橫坐標為
的橫坐標為![]() .
.
(1)求此拋物線的表達式;
(2)過點![]() 作
作![]() 軸,垂足為點
軸,垂足為點![]() ,
,![]() 交
交![]() 于點
于點![]() .試探究點P在運動過程中,是否存在這樣的點
.試探究點P在運動過程中,是否存在這樣的點![]() ,使得以
,使得以![]() 為頂點的三角形是等腰三角形.若存在,請求出此時點
為頂點的三角形是等腰三角形.若存在,請求出此時點![]() 的坐標,若不存在,請說明理由;
的坐標,若不存在,請說明理由;
(3)過點![]() 作
作![]() ,垂足為點
,垂足為點![]() .請用含
.請用含![]() 的代數式表示線段
的代數式表示線段![]() 的長,并求出當
的長,并求出當![]() 為何值時
為何值時![]() 有最大值,最大值是多少?
有最大值,最大值是多少?
【答案】(1) ![]() ;(2) 存在,
;(2) 存在,![]() 或
或 ;;(3) 當
;;(3) 當![]() 時,
時,![]() 的最大值為:
的最大值為:![]() .
.
【解析】
(1)由二次函數交點式表達式,即可求解;
(2)分![]() 三種情況,分別求解即可;
三種情況,分別求解即可;
(3)由![]() 即可求解.
即可求解.
解:(1)由二次函數交點式表達式得:![]() ,
,
即:![]() ,解得:
,解得:![]() ,
,
則拋物線的表達式為![]() ;
;
(2)存在,理由:
點![]() 的坐標分別為
的坐標分別為![]() ,
,
則![]() ,
,
將點![]() 的坐標代入一次函數表達式:
的坐標代入一次函數表達式:![]() 并解得:
并解得:![]() …①,
…①,
同理可得直線AC的表達式為:![]() ,
,
設直線![]() 的中點為
的中點為![]() ,過點
,過點![]() 與
與![]() 垂直直線的表達式中的
垂直直線的表達式中的![]() 值為
值為![]() ,
,
同理可得過點![]() 與直線
與直線![]() 垂直直線的表達式為:
垂直直線的表達式為:![]() …②,
…②,
①當![]() 時,如圖1,
時,如圖1,
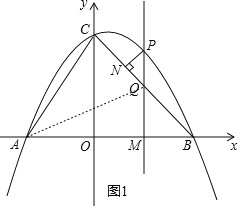
則![]() ,
,
設:![]() ,則
,則![]() ,
,
由勾股定理得:![]() ,解得:
,解得:![]() 或4(舍去4),
或4(舍去4),
故點![]() ;
;
②當![]() 時,如圖1,
時,如圖1,
![]() ,則
,則![]() ,
,
則![]() ,
,
故點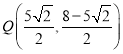 ;
;
③當![]() 時,
時,
聯立①②并解得:![]() (舍去);
(舍去);
故點Q的坐標為:![]() 或
或 ;
;
(3)設點![]() ,則點
,則點![]() ,
,
∵![]() ,
,
∴![]() ,
,
![]() ,
,
∵![]() ,
,
∴![]() 有最大值,
有最大值,
當![]() 時,
時,![]() 的最大值為:
的最大值為:![]() .
.


 期末好成績系列答案
期末好成績系列答案 99加1領先期末特訓卷系列答案
99加1領先期末特訓卷系列答案 百強名校期末沖刺100分系列答案
百強名校期末沖刺100分系列答案 好成績1加1期末沖刺100分系列答案
好成績1加1期末沖刺100分系列答案 金狀元績優好卷系列答案
金狀元績優好卷系列答案科目:初中數學 來源: 題型:
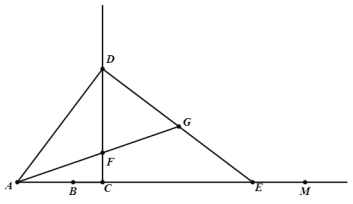
【題目】如圖,射線AM上有一點B,AB=6.點C是射線AM上異于B的一點,過C作CD⊥AM,且CD=![]() AC.過D點作DE⊥AD,交射線AM于E. 在射線CD取點F,使得CF=CB,連接AF并延長,交DE于點G.設AC=3x.
AC.過D點作DE⊥AD,交射線AM于E. 在射線CD取點F,使得CF=CB,連接AF并延長,交DE于點G.設AC=3x.
(1) 當C在B點右側時,求AD、DF的長.(用關于x的代數式表示)
(2)當x為何值時,△AFD是等腰三角形.
(3)若將△DFG沿FG翻折,恰使點D對應點![]() 落在射線AM上,連接
落在射線AM上,連接![]() ,
,![]() .此時x的值為 (直接寫出答案)
.此時x的值為 (直接寫出答案)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)問題發現如圖1,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,連接
,連接![]() 交于點
交于點![]() .填空:①
.填空:①![]() 的值為______;②
的值為______;②![]() 的度數為______.
的度數為______.
(2)類比探究如圖2,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,連接
,連接![]() 交
交![]() 的延長線于點
的延長線于點![]() .請判斷
.請判斷![]() 的值及
的值及![]() 的度數,并說明理由;
的度數,并說明理由;
(3)拓展延伸在(2)的條件下,將![]() 繞點
繞點![]() 在平面內旋轉,
在平面內旋轉,![]() 所在直線交于點
所在直線交于點![]() ,若
,若![]() ,
,![]() ,請直接寫出當點
,請直接寫出當點![]() 與點
與點![]() 在同一條直線上時
在同一條直線上時![]() 的長.
的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
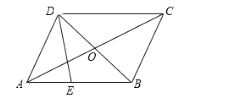
【題目】如圖,在平行四邊形ABCD中,對角線AC、BD相交于點O.E為邊AB上一點,且BE = 2AE.設![]() ,
,![]() .
.
(1)填空:向量![]() ;
;
(2)如果點F是線段OC的中點,那么向量![]() ,并在圖中畫出向量
,并在圖中畫出向量![]() 在向量
在向量![]() 和
和![]() 方向上的分向量.
方向上的分向量.
注:本題結果用向量![]() 的式子表示.畫圖不要求寫作法,但要指出所作圖中表示結論的向量.
的式子表示.畫圖不要求寫作法,但要指出所作圖中表示結論的向量.
查看答案和解析>>
科目:初中數學 來源: 題型:
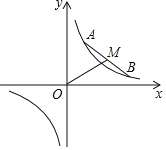
【題目】如圖,在平面直角坐標系中,點![]() ,
,![]() 在反比例函數
在反比例函數![]() 的圖象上運動,且始終保持線段
的圖象上運動,且始終保持線段![]() 的長度不變.
的長度不變.![]() 為線段
為線段![]() 的中點,連接
的中點,連接![]() .則線段
.則線段![]() 長度的最小值是_____(用含
長度的最小值是_____(用含![]() 的代數式表示).
的代數式表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市居民用水實行以戶為單位的三級階梯收費辦法:
第一級:居民每戶每月用水![]() 噸以內含
噸以內含![]() 噸,每噸收水費
噸,每噸收水費![]() 元;
元;
第二級:居民每戶每月用水超過![]() 噸但不超過
噸但不超過![]() 噸,未超過
噸,未超過![]() 的部分按照第一級標準收費,超過部分每噸收水費
的部分按照第一級標準收費,超過部分每噸收水費![]() 元;
元;
第三級:居民每戶每月用水超過![]() 噸,未超過
噸,未超過![]() 噸的部分按照第一、二級標準收費,超過部分每噸收水費
噸的部分按照第一、二級標準收費,超過部分每噸收水費![]() 元;
元;
設一戶居民月用水![]() 噸,應繳水費
噸,應繳水費![]() 元,
元,![]() 與
與![]() 之間的函數關系如圖所示,
之間的函數關系如圖所示,
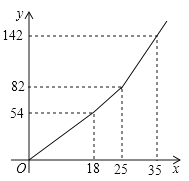
(Ⅰ)根據圖象直接作答:![]() ___________,
___________,![]() _______________,
_______________,![]() _______________;
_______________;
(Ⅱ)求當![]() 時,
時,![]() 與
與![]() 之間的函數關系式;
之間的函數關系式;
(Ⅲ)把上述水費階梯收費辦法稱為方案①,假設還存在方案②;居民每戶月用水一律按照每噸![]() 元的標準繳費.當居民用戶月用水超過
元的標準繳費.當居民用戶月用水超過![]() 噸時,請你根據居民每戶月用水量的大小設計出對居民繳費最實惠的方案.
噸時,請你根據居民每戶月用水量的大小設計出對居民繳費最實惠的方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,D、F分別是BC、AC邊的中點,連接DA、DF,且AD=2DF,過點B作AD的平行線交FD的延長線于點E.
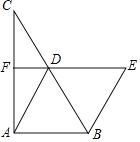
(1)求證:四邊形ABED為菱形;
(2)若BD=6,∠E=60°,求四邊形ABEF的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,李林和王聰兩人在玩轉盤游戲時,分別把轉盤![]() ,
,![]() 分成3等份和4等份,并標上數字(如圖所示).游戲規則:同時轉動兩個轉盤,當兩轉盤停止后,若指針所指兩個數字之和小于4,則李林獲勝;若數字之和大于4,則王聰獲勝,如果指針落在分割線上,則需要重新轉動轉盤.
分成3等份和4等份,并標上數字(如圖所示).游戲規則:同時轉動兩個轉盤,當兩轉盤停止后,若指針所指兩個數字之和小于4,則李林獲勝;若數字之和大于4,則王聰獲勝,如果指針落在分割線上,則需要重新轉動轉盤.
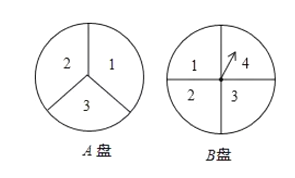
(1)用列表法或畫樹狀圖法中的一種方法,求所有可能出現的結果.
(2)該游戲規則對雙方公平嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了綠化環境,某中學八年級(3班)同學都積極參加了植樹活動,下面是今年3月份該班同學植樹情況的扇形統計圖和不完整的條形統計圖:
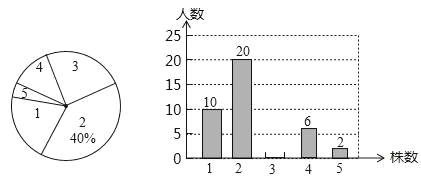
請根據以上統計圖中的信息解答下列問題.
(1)植樹3株的人數為 ;
(2)扇形統計圖中植樹為1株的扇形圓心角的度數為 ;
(3)該班同學植樹株數的中位數是
(4)小明以下方法計算出該班同學平均植樹的株數是:(1+2+3+4+5)÷5=3(株),根據你所學的統計知識
判斷小明的計算是否正確,若不正確,請寫出正確的算式,并計算出結果
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com