
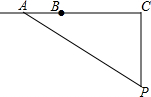
 如圖,l為一條東西方向的筆直公路,一輛小汽車XRS在這段限速為80千米/小時的公路上由西向東勻速行駛,依次經過點A、B、C,P是一個觀測點,PC⊥l,PC=60米,tan∠APC=$\frac{4}{3}$,∠BPC=45°,測得該車從點A行駛到點B所用時間為1秒.
如圖,l為一條東西方向的筆直公路,一輛小汽車XRS在這段限速為80千米/小時的公路上由西向東勻速行駛,依次經過點A、B、C,P是一個觀測點,PC⊥l,PC=60米,tan∠APC=$\frac{4}{3}$,∠BPC=45°,測得該車從點A行駛到點B所用時間為1秒.分析 (1)由三角函數求出AC,證出△BCP是等腰直角三角形,得出BC=PC=60米,求出AB=AC-BC=20米即可;
(2)求出該車從點A行駛到點B的速度為20米/秒=72千米/小時<80千米/小時,即可得出結果.
解答 解:如圖所示: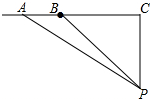
(1)∵PC⊥l,PC=60米,tan∠APC=$\frac{4}{3}$=$\frac{AC}{PC}$,
∴AC=80米,
∵∠BPC=45°,
∴△BCP是等腰直角三角形,
∴BC=PC=60米,
∴AB=AC-BC=20米,
答:A、B兩點間的距離為20米;
(2)該車不超過限速;理由如下:
由題意得:該車從點A行駛到點B所用時間為1秒,
∴該車從點A行駛到點B的速度為20米/秒=72千米/小時<80千米/小時,
∴該車不超過限速.
點評 本題考查了解直角三角形的應用、等腰直角三角形的判定與性質;熟練掌握解直角三角形,由三角函數求出AC是解決問題(1)的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
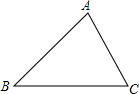 如圖,已知△ABC中,AC=6,∠ABC=45°.
如圖,已知△ABC中,AC=6,∠ABC=45°.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知∠BOC=30°,OM平分∠AOC,ON平分∠BOC,
已知∠BOC=30°,OM平分∠AOC,ON平分∠BOC,查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,一次函數y=ax+b的圖象與反比例函數$y=\frac{k}{x}$的圖象交于A(-2,m),B(5,-2)兩點,與x軸交于C點,過A作AD⊥x軸于D.
如圖,一次函數y=ax+b的圖象與反比例函數$y=\frac{k}{x}$的圖象交于A(-2,m),B(5,-2)兩點,與x軸交于C點,過A作AD⊥x軸于D.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com