
 如圖,一次函數(shù)y=ax+b的圖象與反比例函數(shù)$y=\frac{k}{x}$的圖象交于A(-2,m),B(5,-2)兩點,與x軸交于C點,過A作AD⊥x軸于D.
如圖,一次函數(shù)y=ax+b的圖象與反比例函數(shù)$y=\frac{k}{x}$的圖象交于A(-2,m),B(5,-2)兩點,與x軸交于C點,過A作AD⊥x軸于D.分析 (1)先把B點坐標代入$y=\frac{k}{x}$求出k的值,從而得到反比例函數(shù)解析式為y=-$\frac{10}{x}$;再把A(-2,m)代入y=-$\frac{10}{x}$求出m得到A(-2,5),然后利用待定系數(shù)法求一次函數(shù)解析式;
(2)如圖,先確定C(3,0),(-2,0),然后根據(jù)三角形面積公式,利用S△ADB=S△ADC+S△BCD進行計算.
解答 解:(1)把B(5,-2)代入$y=\frac{k}{x}$得k=5×(-2)=-10,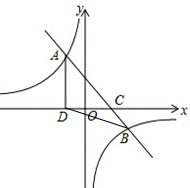
所以反比例函數(shù)解析式為y=-$\frac{10}{x}$;
把A(-2,m)代入y=-$\frac{10}{x}$得-2m=-10,解得m=5,則A(-2,5),
把A(-2,5),B(5,-2)代入y=ax+b得$\left\{\begin{array}{l}{-2a+b=5}\\{5a+b=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-1}\\{b=3}\end{array}\right.$,
所以一次函數(shù)解析式:y=-x+3;
(2)如圖,當y=0時,-x+3=0,解得x=3,則C(3,0),而(-2,0),
所以S△ADB=S△ADC+S△BCD
=$\frac{1}{2}$•(3+2)•5+$\frac{1}{2}$•(3+2)•2
=$\frac{35}{2}$.
點評 本題考查了反比例函數(shù)與一次函數(shù)的交點問題:求反比例函數(shù)與一次函數(shù)的交點坐標,把兩個函數(shù)關系式聯(lián)立成方程組求解,若方程組有解則兩者有交點,方程組無解,則兩者無交點.也考查了觀察函數(shù)圖象的能力.


 口算小狀元口算速算天天練系列答案
口算小狀元口算速算天天練系列答案科目:初中數(shù)學 來源: 題型:解答題
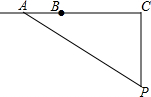 如圖,l為一條東西方向的筆直公路,一輛小汽車XRS在這段限速為80千米/小時的公路上由西向東勻速行駛,依次經(jīng)過點A、B、C,P是一個觀測點,PC⊥l,PC=60米,tan∠APC=$\frac{4}{3}$,∠BPC=45°,測得該車從點A行駛到點B所用時間為1秒.
如圖,l為一條東西方向的筆直公路,一輛小汽車XRS在這段限速為80千米/小時的公路上由西向東勻速行駛,依次經(jīng)過點A、B、C,P是一個觀測點,PC⊥l,PC=60米,tan∠APC=$\frac{4}{3}$,∠BPC=45°,測得該車從點A行駛到點B所用時間為1秒.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
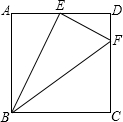 在正方形ABCD中,點E為AD中點,DF=$\frac{1}{4}$CD,則下列說法:(1)BE⊥EF;(2)圖中有3對相似三角形;(3)E到BF的距離為$\frac{1}{2}$AB;(4)$\frac{{S}_{△BEF}}{{S}_{△BCF}}$=$\frac{5}{7}$.其中正確的有( )
在正方形ABCD中,點E為AD中點,DF=$\frac{1}{4}$CD,則下列說法:(1)BE⊥EF;(2)圖中有3對相似三角形;(3)E到BF的距離為$\frac{1}{2}$AB;(4)$\frac{{S}_{△BEF}}{{S}_{△BCF}}$=$\frac{5}{7}$.其中正確的有( )| A. | 4個 | B. | 3個 | C. | 2個 | D. | 1個 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 如圖,已知三點A、B、C,請用尺規(guī)作圖完成(保留作圖痕跡)
如圖,已知三點A、B、C,請用尺規(guī)作圖完成(保留作圖痕跡)查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com