
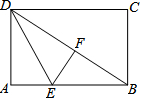
 如圖,折疊長方形紙片ABCD,先折出對角線BD,再將AD折疊到BD上,得到折痕DE,點A的對應點是點F,若AB=8,BC=6,則AE的長為3.
如圖,折疊長方形紙片ABCD,先折出對角線BD,再將AD折疊到BD上,得到折痕DE,點A的對應點是點F,若AB=8,BC=6,則AE的長為3. 分析 先利用勾股定理求出BD,再求出DF、BF,設AE=EF=x,在Rt△BEF中,由EB2=EF2+BF2,列出方程即可解決問題.
解答  解:∵四邊形ABCD是矩形,
解:∵四邊形ABCD是矩形,
∴∠A=90°,
∵AB=8,AD=6,
∴BD=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵△DEF是由△DEA翻折得到,
∴DF=AD=6,BF=4,
設AE=EF=x,
在Rt△BEF中,∵EB2=EF2+BF2,
∴(8-x)2=x2+42,
解得x=3,
∴AE=3,
故答案為3.
點評 本題考查矩形的性質、勾股定理等知識,解題時,我們常常設要求的線段長為x,然后根據折疊和軸對稱的性質用含x的代數式表示其他線段的長度,選擇適當的直角三角形,運用勾股定理列出方程求出答案.


科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
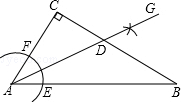 如圖,在△ABC中,∠C=90°,∠CAB=56°,按以下步驟作圖:①以點A為圓心,小于AC長為半徑畫弧,分別交AB、AC于點E、F;②分別以點E、F為圓心,大于$\frac{1}{2}$EF長為半徑畫弧,兩弧相交于點G;③作射線AG,交BC邊于點D.則∠ADC的度數為( )
如圖,在△ABC中,∠C=90°,∠CAB=56°,按以下步驟作圖:①以點A為圓心,小于AC長為半徑畫弧,分別交AB、AC于點E、F;②分別以點E、F為圓心,大于$\frac{1}{2}$EF長為半徑畫弧,兩弧相交于點G;③作射線AG,交BC邊于點D.則∠ADC的度數為( )| A. | 34° | B. | 52° | C. | 58° | D. | 62° |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | BD=CD | B. | ∠B=∠C | C. | AB=AC | D. | ∠BDA=∠CDA |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{-a+b}{-a-b}=\frac{a+b}{a-b}$ | |
| B. | $\frac{0.4a-0.09b}{0.8c+0.06d}=\frac{4a-9b}{8c+6d}$ | |
| C. | $\frac{{{b^2}-{a^2}}}{a+b}=a-b$ | |
| D. | $\frac{{1-\frac{1}{3}a}}{{a+\frac{1}{5}}}=\frac{15-5a}{15a+3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
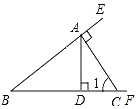 如圖,已知點A是射線BE上一點,過A作CA⊥BE交射線BF于點C,AD⊥BF交射線BF于點D,給出下列結論:
如圖,已知點A是射線BE上一點,過A作CA⊥BE交射線BF于點C,AD⊥BF交射線BF于點D,給出下列結論:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com