
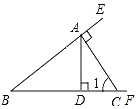
 如圖,已知點A是射線BE上一點,過A作CA⊥BE交射線BF于點C,AD⊥BF交射線BF于點D,給出下列結論:
如圖,已知點A是射線BE上一點,過A作CA⊥BE交射線BF于點C,AD⊥BF交射線BF于點D,給出下列結論:分析 根據垂直定義可得∠BAC=90°,∠ADC=∠ADB=∠CAE=90°,然后再根據余角定義和補角定義進行分析即可.
解答  解:∵CA⊥BE,
解:∵CA⊥BE,
∴∠BAC=90°,
∴∠B+∠1=90°,
∴∠1是∠B的余角,故①正確;
∵AD⊥BF,
∴∠ADC=∠ADB=90°,
∴∠B+∠BAD=90°,∠1+∠DAC=90°,
∵∠BAC=90°,
∴∠BAD+∠CAD=90°,
∴圖中互余的角共有4對,故②正確;
∵∠1+∠ACF=180°,
∴∠1的補角是∠ACF,
∵∠1+∠DAC=90°,∠BAD+∠DAC=90°,
∴∠1=∠BAD,
∵∠BAD+∠DAE=180°,
∴∠1+∠DAE=180°,
∴∠1的補角有∠DAE,故③說法錯誤;
∵∠ADB=90°,∠ADC=90°,∠BAC=∠CAF=90°,
∴∠ADC,∠BAC,∠CAE和∠ADB互補,故④說法正確.
故答案為:①②④.
點評 此題主要考查了余角和補角,關鍵是掌握兩角之和為90°時,這兩個角互余;兩角之和為180°時,這兩個角互補.


科目:初中數學 來源: 題型:填空題
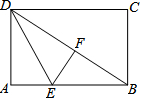 如圖,折疊長方形紙片ABCD,先折出對角線BD,再將AD折疊到BD上,得到折痕DE,點A的對應點是點F,若AB=8,BC=6,則AE的長為3.
如圖,折疊長方形紙片ABCD,先折出對角線BD,再將AD折疊到BD上,得到折痕DE,點A的對應點是點F,若AB=8,BC=6,則AE的長為3.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\left\{\begin{array}{l}{■=8}\\{★=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{■=8}\\{★=5}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{■=5}\\{★=3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{■=3}\\{★=8}\end{array}\right.$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題

| A. | 3個 | B. | 2個 | C. | 1個 | D. | 0個 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
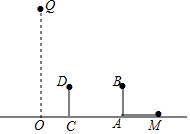 如圖,身高1.6米的小明站在距路燈底部O點10米的點A處,他的身高(線段AB)在路燈下的影子為線段AM,已知路燈燈桿OQ垂直于路面.
如圖,身高1.6米的小明站在距路燈底部O點10米的點A處,他的身高(線段AB)在路燈下的影子為線段AM,已知路燈燈桿OQ垂直于路面.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com