
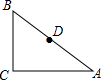
 如圖,在△ABC中,∠C=90°,AC=8,BC=6,D是邊AB的中點,現有一點P位于邊AC上,使得△ADP與△ABC相似,則線段AP的長為4或$\frac{25}{4}$.
如圖,在△ABC中,∠C=90°,AC=8,BC=6,D是邊AB的中點,現有一點P位于邊AC上,使得△ADP與△ABC相似,則線段AP的長為4或$\frac{25}{4}$. 分析 先根據勾股定理求出AB的長,再分△ADP∽△ABC與△ADP∽△ACB兩種情況進行討論即可.
解答  解:∵在△ABC中,∠C=90°,AC=8,BC=6,
解:∵在△ABC中,∠C=90°,AC=8,BC=6,
∴AB=$\sqrt{{8}^{2}+{6}^{2}}$=10.
∵D是邊AB的中點,
∴AD=5.
當△ADP∽△ABC時,$\frac{AD}{AB}$=$\frac{AP}{AC}$,即$\frac{5}{10}$=$\frac{AP}{8}$,解得AP=4;
當△ADP∽△ACB時,$\frac{AD}{AC}$=$\frac{AP}{AB}$,即$\frac{5}{8}$=$\frac{AP}{10}$,解得AP=$\frac{25}{4}$.
故答案為:4或$\frac{25}{4}$.
點評 本題考查的是相似三角形的判定,在解答此題時要注意進行分類討論,不要漏解.


 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:初中數學 來源: 題型:填空題
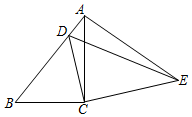 如圖,在△ABC中,∠ACB=90°,AB=9,cosB=$\frac{2}{3}$,把△ABC繞著點C旋轉,使點B與AB邊上的點D重合,點A落在點E,則點A、E之間的距離為4$\sqrt{5}$.
如圖,在△ABC中,∠ACB=90°,AB=9,cosB=$\frac{2}{3}$,把△ABC繞著點C旋轉,使點B與AB邊上的點D重合,點A落在點E,則點A、E之間的距離為4$\sqrt{5}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在平面直角坐標系xOy中,拋物線y=ax2+bx+4與x軸的正半軸相交于點A,與y軸相交于點B,點C在線段OA上,點D在此拋物線上,CD⊥x軸,且∠DCB=∠DAB,AB與CD相交于點E.
如圖,在平面直角坐標系xOy中,拋物線y=ax2+bx+4與x軸的正半軸相交于點A,與y軸相交于點B,點C在線段OA上,點D在此拋物線上,CD⊥x軸,且∠DCB=∠DAB,AB與CD相交于點E.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 投擲一枚均勻的硬幣,正面朝上的概率是$\frac{1}{2}$ | |
| B. | 投擲一枚圖釘,釘尖朝上、朝下的概率一樣 | |
| C. | 投擲一枚均勻的骰子,每一種點數出現的概率都是$\frac{1}{6}$,所以每投6次,一定會出現一次“l點” | |
| D. | 投擲一枚均勻的骰子前默念幾次“出現6點”,投擲結果“出現6點”的可能性就會加大 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,在平面直角坐標系xOy中,已知點A(2,1)和點B(3,0),則sin∠AOB的值等于( )
如圖,在平面直角坐標系xOy中,已知點A(2,1)和點B(3,0),則sin∠AOB的值等于( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com