
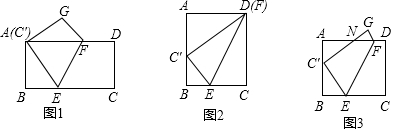
分析 (1)由四邊形ABCD為矩形,得到∠BAD=∠B=∠C=∠D=90°,AB=CD,由翻折的性質得到CD=AG,∠C=∠EAG,FD=FG,根據全等三角形的性質即可得到結論;
(2)設BE=3x,則CE=5x,得到C′E=5x,AD=8x,在Rt△BEC′中,由勾股定理得BC′=4x,由翻折的性質得到∠C=∠GC′E=90°,根據相似三角形的性質得到結論;
(3)設BE=3a,則CE=5a,BC=8a,于是求得AB=6a,根據相似三角形的性質得到C′N=$\frac{10a}{3}$,由翻折的性質CD=C′G,FD=FG=5,然后根據相似三角形的性質即刻得到結論.
解答 解:(1)∵四邊形ABCD為矩形,
∴∠BAD=∠B=∠C=∠D=90°,AB=CD,
由翻折得CD=AG,∠C=∠EAG,FD=FG,
∴∠BAE=∠GAF,
在△ABE與△AGF中,$\left\{\begin{array}{l}{∠B=∠G=90°}\\{AB=AG}\\{∠BAE=∠GAF}\end{array}\right.$,
∴△ABE≌△AGF,
∴BE=GF,
∴BE=DF;
(2)設BE=3x,則CE=5x,∴C′E=5x,AD=8x,
在Rt△BEC′中,由勾股定理得BC′=4x,
由翻折得∠C=∠GC′E=90°,
∴∠BEC′=∠AC′D,
∴△BEC′∽△AC′D,
∴$\frac{BC′}{AD}$=$\frac{BE}{AC′}$,
∴AC′=6x,
∴$\frac{BC}{AB}$=$\frac{8x}{10x}$=$\frac{4}{5}$;
(3)設BE=3a,則CE=5a,BC=8a,
∴AB=6a,
又∵$\frac{BC}{AB}$=$\frac{4}{3}$,
∴BC′=4a,
∴AC′=2a,
易證△BC′E∽△ANC′,
∴$\frac{BE}{AC′}$=$\frac{EC′}{C′N}$,
∴C′N=$\frac{10a}{3}$,
由翻折得CD=C′G,FD=FG=5,
∴C′G=6a,
∴NG=$\frac{8a}{3}$,
又易證△BC′E∽△GNF,
∴$\frac{BE}{GF}$=$\frac{C′B}{NG}$,a=$\frac{5}{2}$,
∴AD=20,
∴AF=15.
點評 本題考查了翻折的性質,矩形的性質,相似三角形的判定和性質,熟練掌握相似三角形的判定和性質是解題的關鍵.


 快樂小博士鞏固與提高系列答案
快樂小博士鞏固與提高系列答案科目:初中數學 來源: 題型:解答題
| 景點 | 頻數 | 頻率 |
| 甲 | 45 | b |
| 乙 | a | 0.3 |
| 丙 | 105 | 0.35 |
| 丁 | 60 | c |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
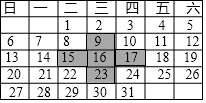 在如圖日歷中,十字框框出了5個數.
在如圖日歷中,十字框框出了5個數.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
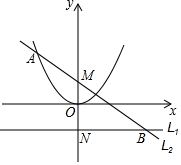 已知a>0,直線L1:y=-$\frac{1}{4a}$與y軸交于點N,點N關于原點的對稱點為點M,過點M的直線L2與拋物線y=ax2在第二象限交于點A,與直線L1交于點B,且MA=MB,平移直線L2,使之與拋物線有唯一公共點,且與y軸交于點P.求證:$\frac{OM}{OP}$為一定值.
已知a>0,直線L1:y=-$\frac{1}{4a}$與y軸交于點N,點N關于原點的對稱點為點M,過點M的直線L2與拋物線y=ax2在第二象限交于點A,與直線L1交于點B,且MA=MB,平移直線L2,使之與拋物線有唯一公共點,且與y軸交于點P.求證:$\frac{OM}{OP}$為一定值.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com