
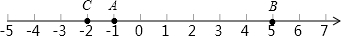
分析 (1)根據點A、B表示的數即可得出點D表示的數,再由兩點間的距離公式即可求出線段CD的長度;
(2)設運動t秒后,點Q可以追上點P,根據點Q追上點P時,兩點代表的數相等即可得出關于t的一元一次方程,解之即可得出結論;
(3)假設存在,設點M表示的數為x,分x≤-2、-2<x≤-1、-1<x≤5和x>5四種情況尋找AM、BM、CM的代數式,令其相加等于10即可得出關于x的一元一次方程,解之結合x的取值范圍即可得出結論.
解答 解:(1)(-1+5)÷2=2;
CD=2-(-2)=4.
故答案為:2;4.
(2)設運動t秒后,點Q可以追上點P,
根據題意得:-0.5t-1=-2t+5,
解得:t=4.
答:運動4秒后,點Q可以追上點P.
(3)假設存在,設點M對應的數為x,
①當x≤-2時,AM+BM+CM=(-1-x)+(-2-x)+(5-x)=10,
解得:x=-$\frac{8}{3}$;
②當-2<x≤-1時,AM+BM+CM=(-1-x)+(x+2)+(5-x)=10,
解得:x=-4(舍去);
③當-1<x≤5時,AM+BM+CM=(x+1)+(x+2)+(5-x)=10,
解得:x=2;
④當x>5時,AM+BM+CM=(x+1)+(x+2)+(x-5)=10,
解得:x=4(舍去).
∴假設成立,即在數軸上存在一點M,使M到A、B、C的距離之和等于10,且點M對應的數為-$\frac{8}{3}$或2.
點評 本題考查了一元一次方程的應用、列代數式、數軸以及兩點間的距離,解題的關鍵是:(1)數據數軸上兩點間的距離公式;(2)根據點P、Q兩點表示的數相等找出關于t的一元一次方程;(3)分x≤-2、-2<x≤-1、-1<x≤5和x>5四種情況寫出表示AM、BM、CM的代數式.


 口算小狀元口算速算天天練系列答案
口算小狀元口算速算天天練系列答案 天天練口算系列答案
天天練口算系列答案科目:初中數學 來源: 題型:選擇題
| A. | a、b都是負數 | B. | b是正數,a是負數 | C. | a、b都是正數 | D. | a是正數,b是負數 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
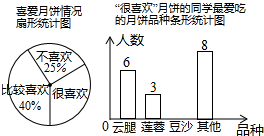 中秋佳節我國有賞月和吃月餅的傳統,某校數學興趣小組為了了解本校學生喜愛月餅的情況,隨機抽取了60名同學進行問卷調查,經過統計后繪制了兩幅尚不完整的統計圖.(注:參與問卷調查的每一位同學在任何一種分類統計中只有一種選擇)
中秋佳節我國有賞月和吃月餅的傳統,某校數學興趣小組為了了解本校學生喜愛月餅的情況,隨機抽取了60名同學進行問卷調查,經過統計后繪制了兩幅尚不完整的統計圖.(注:參與問卷調查的每一位同學在任何一種分類統計中只有一種選擇)查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
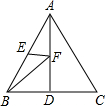 如圖,已知點D、點E分別是等邊三角形ABC中BC、AB邊的中點,AD=5,點F是AD邊上的動點,則BF+EF的最小值為( )
如圖,已知點D、點E分別是等邊三角形ABC中BC、AB邊的中點,AD=5,點F是AD邊上的動點,則BF+EF的最小值為( )| A. | 7.5 | B. | 5 | C. | 4 | D. | 不能確定 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知在矩形ABCD中,AB=2a,把矩形沿直線AC折疊,點B落在點E處,連接DE、BE,△ABE是等邊三角形.
如圖,已知在矩形ABCD中,AB=2a,把矩形沿直線AC折疊,點B落在點E處,連接DE、BE,△ABE是等邊三角形.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
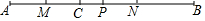 如圖,點C是線段AB上一點,點M、N、P分別是線段AC、BC、AB的中點,AC=3cm,CP=1cm,求:
如圖,點C是線段AB上一點,點M、N、P分別是線段AC、BC、AB的中點,AC=3cm,CP=1cm,求:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com