
 如圖,△ABC內接于⊙O,∠B=60°,CD是⊙O的直徑,點P是CD延長線上的一點,且AP=AC.
如圖,△ABC內接于⊙O,∠B=60°,CD是⊙O的直徑,點P是CD延長線上的一點,且AP=AC.分析 (1)連接OA,根據圓周角定理求出∠AOC,再由OA=OC得出∠ACO=∠OAC=30°,再由AP=AC得出∠P=30°,繼而由∠OAP=∠AOC-∠P,可得出OA⊥PA,從而得出結論;
(2)過點C作CE⊥AB于點E.在Rt△BCE中,∠B=60°,BC=2$\sqrt{3}$,于是得到BE=$\frac{1}{2}$BC=$\sqrt{3}$,CE=3,根據勾股定理得到AC=$\sqrt{A{E}^{2}+C{E}^{2}}$=5,于是得到AP=AC=5.解直角三角形即可得到結論.
解答 (1)證明:連接OA,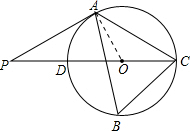
∵∠B=60°,
∴∠AOC=2∠B=120°,
又∵OA=OC,
∴∠OAC=∠OCA=30°,
又∵AP=AC,
∴∠P=∠ACP=30°,
∴∠OAP=∠AOC-∠P=90°,
∴OA⊥PA,
∴PA是⊙O的切線;
(2)解:過點C作CE⊥AB于點E.
在Rt△BCE中,∠B=60°,BC=2$\sqrt{3}$,
∴BE=$\frac{1}{2}$BC=$\sqrt{3}$,CE=3,
∵AB=4+$\sqrt{3}$,
∴AE=AB-BE=4,
∴在Rt△ACE中,AC=$\sqrt{A{E}^{2}+C{E}^{2}}$=5,
∴AP=AC=5.
∴在Rt△PAO中,OA=$\frac{5\sqrt{3}}{3}$,
∴⊙O的半徑為$\frac{5\sqrt{3}}{3}$.
點評 本題考查了切線的判定及圓周角定理,解答本題的關鍵是掌握切線的判定定理、圓周角定理及含30°直角三角形的性質.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:解答題
 如圖,一次函數y=k1x-1的圖象經過A(0,-1)、B(1,0)兩點,與反比例函數y=$\frac{{k}_{2}}{x}$的圖象在第一象限內的交點為M,若△OBM的面積為1.
如圖,一次函數y=k1x-1的圖象經過A(0,-1)、B(1,0)兩點,與反比例函數y=$\frac{{k}_{2}}{x}$的圖象在第一象限內的交點為M,若△OBM的面積為1.查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 作圖:(溫馨提醒:確認后,在答題紙上用黑色水筆描黑)
作圖:(溫馨提醒:確認后,在答題紙上用黑色水筆描黑)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
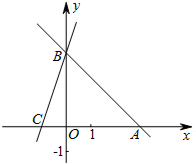 直線AB:y=-x+b分別與x,y軸交于A,B兩點,點A的坐標為 (3,0),過點B的直線交x軸負半軸于點C,且OB:OC=3:1.
直線AB:y=-x+b分別與x,y軸交于A,B兩點,點A的坐標為 (3,0),過點B的直線交x軸負半軸于點C,且OB:OC=3:1.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com