
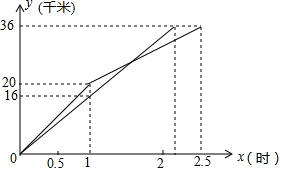
 一次國際龍舟拉力賽中,上午9時,參賽龍舟同時出發,其中甲、乙兩隊在比賽時,路程y(千米)與時間x(小時)的函數關系如圖所示,甲隊在上午11時30分到達終點.
一次國際龍舟拉力賽中,上午9時,參賽龍舟同時出發,其中甲、乙兩隊在比賽時,路程y(千米)與時間x(小時)的函數關系如圖所示,甲隊在上午11時30分到達終點.分析 (1)甲隊在上午11時30分到達終點,共花時間2.5小時,從圖象上看乙隊花時間少,先到終點.從圖象來看,乙隊的路程與時間成正比例關系,甲隊的路程與時間是一個分段函數,即在1小時內是正比例函數,在1到2.5小時是一次函數,可使用待定系數法分別求出.乙隊追上甲隊時,兩隊的路程相等,列出方程可求解;
(2)由圖看出1小時之內,兩隊相距最遠距離是4千米;乙隊追上甲隊后,兩隊的距離也可計算,相比較得出甲、乙兩隊在出發后1小時相距最遠.
解答 解:(1)由題意知,甲上午9時出發,上午11時30分到達終點,耗時2.5小時,
根據圖象可知,乙比甲先到達終點;
當0≤x≤1時,y甲=kx,
將(1,20)代入,得:20=k,即y甲=20x;
當1<x≤2.5時,y甲=kx+b,
將(1,20)、(2.5,36)代入得:
$\left\{\begin{array}{l}{k+b=20}\\{2.5k+b=36}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{32}{3}}\\{b=\frac{28}{3}}\end{array}\right.$,
∴y甲=$\left\{\begin{array}{l}{20x}&{(0≤x≤1)}\\{\frac{32}{3}x+\frac{28}{3}}&{(1<x≤2.5)}\end{array}\right.$,
設y乙=mx,
將(1,16)代入得:10=m,即y乙=16x,
令y甲=y乙,當1<x≤2.5時,$\frac{32}{3}$x+$\frac{28}{3}$=16x,得x=$\frac{7}{4}$,
故出發1小時45分鐘后(或者上午10點45分)乙隊追上甲隊;
(2)由圖象可知小時之內,兩隊相距最遠距離是4千米,
乙隊追上甲隊后,兩隊的距離是16x-($\frac{32}{3}$x+$\frac{28}{3}$)=$\frac{16}{3}$x+$\frac{28}{3}$,
∴當x為最大,即x=$\frac{36}{16}$=$\frac{9}{4}$時,$\frac{16}{3}$x+$\frac{28}{3}$最大,
此時最大距離為$\frac{9}{4}$×$\frac{16}{3}$-$\frac{28}{3}$=$\frac{8}{3}$<4,
所以比賽過程中,甲、乙兩隊在出發后1小時(或者上午10時)相距最遠.
點評 本題考查一次函數的應用,熟練掌握用待定系數法求一次函數關系式并將實際問題轉化為一次函數的問題求解是解題的關鍵.


科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\sqrt{10}$是無理數 | B. | $3<\sqrt{10}<4$ | ||
| C. | 10的平方根是$\sqrt{10}$ | D. | $\sqrt{10}$是10的算術平方根 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
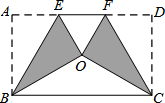 將矩形紙片ABCD按如圖方式折疊,BE、CF為折痕,折疊后點A和點D都落在點O處,若△EOF是等邊三角形,則$\frac{AB}{AD}$的值為$\frac{\sqrt{3}}{3}$.
將矩形紙片ABCD按如圖方式折疊,BE、CF為折痕,折疊后點A和點D都落在點O處,若△EOF是等邊三角形,則$\frac{AB}{AD}$的值為$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com