
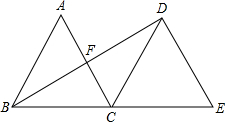
 如圖,△ABC是邊長為2的等邊三角形,將△ABC沿直線BC向右平移,使點B與點C重合,得到△DCE,連接BD,交AC于點F.求線段BD的長.
如圖,△ABC是邊長為2的等邊三角形,將△ABC沿直線BC向右平移,使點B與點C重合,得到△DCE,連接BD,交AC于點F.求線段BD的長. 分析 由平移的性質可知BE=2BC=4,DE=AC=2,故可得出BD⊥DE,由∠E=∠ACB=60°可知AC∥DE,根據勾股定理即可得出BD的長.
解答 解:∵正△ABC沿直線BC向右平移得到正△DCE,
∴BE=2BC=4,BC=CD,DE=AC=2,∠E=∠ACB=∠DCE=∠ABC=60°,
∴∠DBE=$\frac{1}{2}$∠DCE=30°,
∴∠BDE=90°.
在Rt△BDE中,由勾股定理得$BD=\sqrt{B{E^2}-D{E^2}}=\sqrt{{4^2}-{2^2}}=2\sqrt{3}$.
點評 本題考查的是等邊三角形的性質及平移的性質,熟知圖形平移后的圖形與原圖形全等的性質是解答此題的關鍵.


 奪冠金卷全能練考系列答案
奪冠金卷全能練考系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
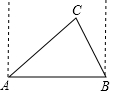 某次軍事演習中,有三艘軍艦在同一時刻向指揮所報告:A軍艦說B軍艦在它的正東方向,C軍艦在它的北偏東60°方向;B軍艦說C軍艦在它的北偏西30°方向,C軍艦說它到B軍艦的距離比它到A軍艦的距離近30海里,求A,B軍艦的距離?(結果精確到0.1海里,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
某次軍事演習中,有三艘軍艦在同一時刻向指揮所報告:A軍艦說B軍艦在它的正東方向,C軍艦在它的北偏東60°方向;B軍艦說C軍艦在它的北偏西30°方向,C軍艦說它到B軍艦的距離比它到A軍艦的距離近30海里,求A,B軍艦的距離?(結果精確到0.1海里,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,四邊形ABCD是正方形,BM=DF,AF垂直AM,M、B、C在一條直線上,且△AEM與△AEF恰好關于AE所在直線成軸對稱,已知EF=x,正方形邊長為y.
如圖,四邊形ABCD是正方形,BM=DF,AF垂直AM,M、B、C在一條直線上,且△AEM與△AEF恰好關于AE所在直線成軸對稱,已知EF=x,正方形邊長為y.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 門票類別 | 散客票 | 團隊票A | 團隊票B |
| 購票要求 | 超過50人但不超過100人 | 超過100人 | |
| 票價(元/人) | 80元/人 | 70元/人 | 60元/人 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
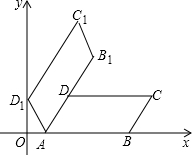 如圖,?ABCD的頂點A,B的坐標分別為(1,0),(5,0),∠DAB=60°,AD=2.
如圖,?ABCD的頂點A,B的坐標分別為(1,0),(5,0),∠DAB=60°,AD=2.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com