
 如圖,四邊形ABCD是正方形,BM=DF,AF垂直AM,M、B、C在一條直線上,且△AEM與△AEF恰好關于AE所在直線成軸對稱,已知EF=x,正方形邊長為y.
如圖,四邊形ABCD是正方形,BM=DF,AF垂直AM,M、B、C在一條直線上,且△AEM與△AEF恰好關于AE所在直線成軸對稱,已知EF=x,正方形邊長為y.分析 (1)利用旋轉的定義求解;
(2)由于△AEM≌△AEF,則EF=EM,即x=BE+BM=DF+BE,則根據三角形面積公式得到S△AME=$\frac{1}{2}$xy,然后利用S△CEF=S正方形ABCD-S△AEF-S△ABE-S△ADF可表示出△EFC的面積.
解答 解:(1)圖中△ADF可以繞點A按順時針方向旋轉90°后能夠與△ABM重合;
故答案為:A、90°,ABM.
(2)∵△AEM與△AEF恰好關于所在直線成軸對稱,
∴EF=EM,
即x=BE+BM,
∵BM=DF,
∴x=DF+BE,
∴S△AME=$\frac{1}{2}$•AB•ME=$\frac{1}{2}$xy,
S△CEF=S正方形ABCD-S△AEF-S△ABE-S△ADF
=y2-$\frac{1}{2}$xy-$\frac{1}{2}$•y•BE-$\frac{1}{2}$•y•DF
=y2-$\frac{1}{2}$xy-$\frac{1}{2}$•y(BE+DF)
=y2-$\frac{1}{2}$xy-$\frac{1}{2}$•y•x
=y2-xy.
點評 本題考查了旋轉的性質:對應點到旋轉中心的距離相等;對應點與旋轉中心所連線段的夾角等于旋轉角;旋轉前、后的圖形全等.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
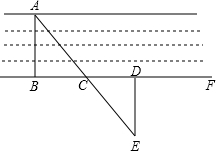 如圖,要測量河兩岸相對的兩點A、B的距離,先在AB的垂線BF上取兩點C、D,使CD=BC,再作出BF的垂線,并在這條垂線上取一點E,使A、C、E在一條直線上(如圖所示),測得ED的長就是A、B之間的距離,請你說明理由.
如圖,要測量河兩岸相對的兩點A、B的距離,先在AB的垂線BF上取兩點C、D,使CD=BC,再作出BF的垂線,并在這條垂線上取一點E,使A、C、E在一條直線上(如圖所示),測得ED的長就是A、B之間的距離,請你說明理由.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 優惠 條件 | 一次性購物不超過200元 | 一次性購物超過200元,但不超過500元 | 一次性購物超過500元 |
| 優惠 辦法 | 沒有優惠 | 全部按九折優惠 | 其中500元仍按九折優惠,超過500元部分按八折優惠 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
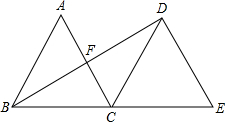 如圖,△ABC是邊長為2的等邊三角形,將△ABC沿直線BC向右平移,使點B與點C重合,得到△DCE,連接BD,交AC于點F.求線段BD的長.
如圖,△ABC是邊長為2的等邊三角形,將△ABC沿直線BC向右平移,使點B與點C重合,得到△DCE,連接BD,交AC于點F.求線段BD的長.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
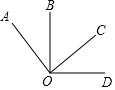 如圖,以點O為端點按順時針方向依次作射線OA、OB、OC、OD,且∠AOC=∠BOD=α(0°<α<180°)
如圖,以點O為端點按順時針方向依次作射線OA、OB、OC、OD,且∠AOC=∠BOD=α(0°<α<180°)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com