
如圖,在平面直角坐標系xOy中,頂點為M的拋物線是由拋物線y=x2﹣3向右平移一個單位后
得到的,它與y軸負半軸交于點A,點B在該拋物線上,且橫坐標為3.

(1)求點M、A、B坐標;
(2)連結AB、AM、BM,求∠ABM的正切值;
(3)點P是頂點為M的拋物線上一點,且位于對稱軸的右側,設PO與x正半軸的夾角為α,當α=∠ABM時,求P點坐標.
見解析
【解析】
試題分析:(1)根據函數平移的規律可得平移后的拋物線解析式是y=(x-1)2-3,所以頂點M的坐標(1,-3),把x=0, x=3分別代入y=(x-1)2-3可求出A點的坐標(0,-2)和點B的坐標(3,1);
(2)過點B作BE⊥AO于E,過點M作MF⊥AO于M,根據EB=EA=3得∠EAB=∠EBA=45°,同理求出∠FAM=∠FMA=45°,然后根據△ABE∽△AMF求出 即可;(3)過點P作PH⊥x軸于H,分兩種情況討論:點P在x軸的上方和下方.
即可;(3)過點P作PH⊥x軸于H,分兩種情況討論:點P在x軸的上方和下方.
試題解析:(1)拋物線y=x2-3向右平移一個單位后得到的函數解析式為y=(x-1)2-3,
頂點M(1,-3),
令x=0,則y=(0-1)2-3=-2,
點A(0,-2),
x=3時,y=(3-1)2-3=4-3=1,
點B(3,1);
(2)過點B作BE⊥AO于E,過點M作MF⊥AO于M,

∵EB=EA=3,
∴∠EAB=∠EBA=45°,
同理可求∠FAM=∠FMA=45°,
∴△ABE∽△AMF,
∴ =
= =
= ,
,
又∵∠BAM=180°-45°×2=90°,
∴tan∠ABM= =
= ;
;
(3)過點P作PH⊥x軸于H,
∵y=(x-1)2-3=x2-2x-2,
∴設點P(x,x2-2x-2),
①點P在x軸的上方時, =
= ,
,
整理得,3x2-7x-6=0,
解得x1=- (舍去),x2=3,
(舍去),x2=3,
∴點P的坐標為(3,1);
②點P在x軸下方時, =
= ,
,
整理得,3x2-5x-6=0,
解得x1= (舍去),x2=
(舍去),x2= ,
,
x= 時,x2-2x-2=-
時,x2-2x-2=- ×
× =-
=- ,
,
∴點P的坐標為( ,-
,- ),
),
綜上所述,點P的坐標為(3,1)或( ,-
,- ).
).
考點:1.二次函數圖象的平移;2.求拋物線與坐標軸的交點;3.相似三角形的判定與性質;4.銳角三角形函數.


科目:初中數學 來源:2014-2015學年安徽濉溪城關中心學校八年級上學期第三次月考數學卷(解析版) 題型:選擇題
點P(-3,4)到y軸的距離是 ( )
A.4 B.3 C.-3 D.5
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省鹽城市阜寧縣九年級上學期期中學情調研數學試卷(解析版) 題型:選擇題
△ABC為⊙O的內接三角形,若∠AOC=160°,則∠ABC的度數是 .
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省鹽城市阜寧縣九年級上學期期中學情調研數學試卷(解析版) 題型:選擇題
已知關于 的方程
的方程 ,下列說法正確的是( )
,下列說法正確的是( )
A.當 時,方程無解
時,方程無解
B.當 時,方程有一個實數解
時,方程有一個實數解
C.當 時,方程有兩個相等的實數解
時,方程有兩個相等的實數解
D.當 時,方程總有兩個不相等的實數解
時,方程總有兩個不相等的實數解
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省興化顧莊等三校九年級上學期12月月考數學試卷(解析版) 題型:解答題
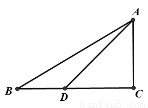
在Rt△ABC中,∠C=900, tanB= , ∠ADC=45°,DC=6,求BD的長.
, ∠ADC=45°,DC=6,求BD的長.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省興化顧莊等三校九年級上學期12月月考數學試卷(解析版) 題型:填空題
在等邊△ABC中,點D、E分別在AB、AC邊上,且DE∥BC.如果BC=8 cm,AD:DB=1:3,那
么△ADE的周長等于_______cm.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年福建省九年級上學期第三次教學質量監測數學試卷(解析版) 題型:解答題
(本題滿分10分)某市政府大力扶持大學生創業.李明在政府的扶持下投資銷售一種進價為每件20元的護眼臺燈.銷售過程中發現,每月銷售量y(件)與銷售單價x(元)之間的關系可近似的看作一次函數: .
.
(1)設李明每月獲得利潤為w(元),當銷售單價定為多少元時,每月可獲得最大利潤?
(2)如果李明想要每月獲得2000元的利潤,那么銷售單價應定為多少元?
(3)根據物價部門規定,這種護眼臺燈的銷售單價不得高于32元,如果李明想要每月獲得的利潤不低于2000元,那么他每月的成本最少需要多少元?(成本=進價×銷售量)
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省興化顧莊三校八年級上學期12月月考數學試卷(解析版) 題型:填空題
如圖,在△ABC中,∠ACB=90°,沿CD折疊△CBD,使點B恰好落在AC邊上的點E處.
若∠A=28°,則∠ADE= °

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com