
 如圖,在四邊形ABCD中,∠DAB=60°,∠BCD=150°,對角線AC平分∠DAB,AC=6,則△DAB的面積為9$\sqrt{3}$.
如圖,在四邊形ABCD中,∠DAB=60°,∠BCD=150°,對角線AC平分∠DAB,AC=6,則△DAB的面積為9$\sqrt{3}$. 分析 作高線DF,根據∠DAF=60°,設AF=x,則AD=2x,DF=$\sqrt{3}$x,證明△ADC∽△ACB,則$\frac{AD}{AC}=\frac{AC}{AB}$,得
AD•AB=AC2=62=36,整體代入面積公式可得結論.
解答 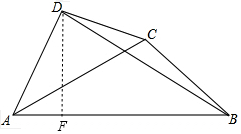 解:∵AC平分∠DAB,∠DAB=60°,
解:∵AC平分∠DAB,∠DAB=60°,
∴∠DAC=∠BAC=30°,
∴∠ADC+∠ACD=150°,
∵∠DCB=150°,
∴∠ACB+∠ACD=150°,
∴∠ADC=∠ACB,
∴△ADC∽△ACB,
∴$\frac{AD}{AC}=\frac{AC}{AB}$,
∴AD•AB=AC2=62=36,
過D作DF⊥AB于F,
在Rt△ADF中,∠DAF=60°,
∴∠ADF=30°,
設AF=x,則AD=2x,DF=$\sqrt{3}$x,
∴S△ABD=$\frac{1}{2}$AB•DF=$\frac{1}{2}$AB$•\sqrt{3}$x=$\frac{\sqrt{3}}{2}$AB•2x$•\frac{1}{2}$=$\frac{\sqrt{3}}{4}$AB•AD=$\frac{\sqrt{3}}{4}$×36=9$\sqrt{3}$;
故答案為:9$\sqrt{3}$.
點評 本題考查了相似三角形的性質和判定、角平分線的定義、直角三角形30°角的性質,本題證明△ADC∽△ACB是關鍵,還運用了整體的思想,使問題得以解決.


科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 0.3,0.4,0.5 | B. | 4,5,6 | C. | $\frac{3}{5}$,$\frac{4}{5}$,1 | D. | 24,45,51 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\sqrt{24}$ | B. | $\sqrt{0.3}$ | C. | $\sqrt{\frac{1}{3}}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
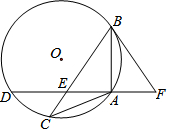 如圖,△ABC內接于⊙O,AB=AC,過點A作AD⊥AB交⊙O于點D,交BC于點E,點F在DA的延長線上,且∠ABF=∠C.
如圖,△ABC內接于⊙O,AB=AC,過點A作AD⊥AB交⊙O于點D,交BC于點E,點F在DA的延長線上,且∠ABF=∠C.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com