
 在△ABC中,∠A=60°,∠ABC,∠ACB所對的邊b,c滿足b2+c2-4(b+c)+8=0.
在△ABC中,∠A=60°,∠ABC,∠ACB所對的邊b,c滿足b2+c2-4(b+c)+8=0.分析 (1)由b2+c2-2(b+c)+2=0,可以判定b=c,∠A=60°可以確定△ABC是邊長為1的等邊三角形;
(2)連接DE,點D、E分別是邊AC、AB邊上的中點,所以DE∥BC,DE=$\frac{1}{2}$BC,∴△DEO∽△BOC,即可得到答案.
解答 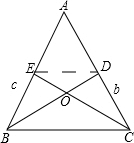 解:(1)∵b2+c2-4(b+c)+8=0,
解:(1)∵b2+c2-4(b+c)+8=0,
∴(b-2)2+(c-2)2=0,
∴b=c=2,
又∵∠A=60°,
所以△ABC是邊長為2的等邊三角形;
(2)連接DE,
∵點D、E分別是邊AC、AB邊上的中點,
所以DE∥BC,DE=$\frac{1}{2}$BC,
∵DE∥BC,
∴△DEO∽△BOC,
∴$\frac{DE}{BC}$=$\frac{OD}{OB}$=$\frac{1}{2}$
點評 本題考查因式分解的應用以及相似三角形的綜合應用,解答本題的關在在于熟記公式的轉化和相似三角形的判定方法和性質的綜合應用.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 45、45、90 | B. | 30、60、90 | C. | 25、25、130 | D. | 36、72、72 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | y1<y2 | B. | y1>y2 | C. | y1=y2 | D. | 不能確定 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
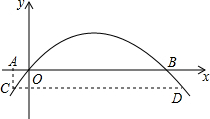 如圖是某拱形大橋的示意圖,橋拱與橋面的交點為O,B,以點O為原點,水平直線OB為x軸,建立平面直角坐標系,橋的拱形可以近似看成拋物線y=-$\frac{1}{400}$(x-80)2+16,橋拱與橋墩AC的交點C恰好在水面,有AC⊥x軸.若OA=10米,則橋面離水面的高度AC為$\frac{17}{4}$米.
如圖是某拱形大橋的示意圖,橋拱與橋面的交點為O,B,以點O為原點,水平直線OB為x軸,建立平面直角坐標系,橋的拱形可以近似看成拋物線y=-$\frac{1}{400}$(x-80)2+16,橋拱與橋墩AC的交點C恰好在水面,有AC⊥x軸.若OA=10米,則橋面離水面的高度AC為$\frac{17}{4}$米.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com