
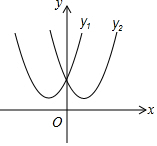
 定義感知:我們把頂點關于y軸對稱,且交于y軸上同一點的兩條拋物線叫做“孿生拋物線”,如圖所示的拋物線y1=x2+2x+2與y2=x2-2x+2是一對“孿生拋物線”.
定義感知:我們把頂點關于y軸對稱,且交于y軸上同一點的兩條拋物線叫做“孿生拋物線”,如圖所示的拋物線y1=x2+2x+2與y2=x2-2x+2是一對“孿生拋物線”.分析 初步運用:(1)①根據“孿生拋物線”的定義即可求解;
②由“孿生拋物線”的意義判斷即可;
(2)由“孿生拋物線”的頂點關于y軸對稱,所以把解析式化成頂點式,求出其“孿生拋物線”;
延伸拓展:由于MM′=4,“孿生拋物線”與y軸的交點A(0,1)到線段MM′的距離為2個單位長度,可得M(2,-1),M′(-2,-1),或M(2,3),M′(-2,3),其“共點”A與M,M′,O三點恰好構成一個面積為12的菱形,且MM′=4,①開口向上時,求出M(-2,3),M′(2,3),設出“孿生拋物線”把共點A(0,1)代入即可求解.
解答 解:初步運用:
(1)①∵把頂點關于y軸對稱,且交于y軸上同一點的兩條拋物線叫做“孿生拋物線”,
∴“孿生拋物線”的兩對稱軸一定關于y軸對稱;
②“孿生拋物線”的開口方向一定相同,原來的說法是錯誤的.
(2)∵拋物線y=2x2-4x-1=2(x-1)2-3,
∴它的“孿生拋物線”為y=2(x+1)2-3=2x2+4x-1,
延伸拓展:∵MM′=4,
∴M(2,y),M′(-2,y),
∵“孿生拋物線”與y軸的交點A(0,1)到線段MM′的距離為2個單位長度,
∴M(2,-1),M′(-2,-1),或M(2,3),M′(-2,3),
∴由此可設“孿生拋物線”的解析式為:y=a(x+2)2-1與y=a(x-2)2-1,
∵點A(0,1)在“孿生拋物線”的圖象上,
∴1=a×22-1,
∴a=$\frac{1}{2}$,
∴“孿生拋物線”的解析式為:y=$\frac{1}{2}$(x+2)2-1與y=$\frac{1}{2}$(x-2)2-1;
由此可設“孿生拋物線”的解析式為:y=a(x+2)2-3與y=a(x-2)2-3,
∵點A(0,1)在“孿生拋物線”的圖象上,
∴1=a×22-3,
∴a=1,
∴“孿生拋物線”的解析式為:y=(x+2)2-3與y=(x-2)2-3.
故答案為:√;×;y=2x2+4x-1.
點評 此題是二次函數綜合題,主要考查了新定義的理解和掌握,二次函數的性質,解決二次函數的方法一樣,解本題的關鍵是掌握“孿生拋物線”的定義.


科目:初中數學 來源: 題型:填空題
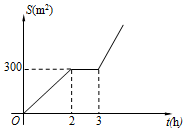 某社區有一塊空地需要綠化,某綠化組承擔了此項任務,該綠化組完成的綠化面積S(單位:m2)與工作時間t(單位:h)之間的函數關系如圖所示.3小時后,綠化組每小時比開始多完成50m2,則當t>3時,S與t的函數關系式為S=200t-300.
某社區有一塊空地需要綠化,某綠化組承擔了此項任務,該綠化組完成的綠化面積S(單位:m2)與工作時間t(單位:h)之間的函數關系如圖所示.3小時后,綠化組每小時比開始多完成50m2,則當t>3時,S與t的函數關系式為S=200t-300.查看答案和解析>>
科目:初中數學 來源: 題型:填空題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
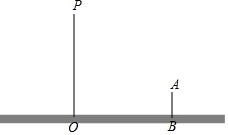 晚上,小亮在廣場乘涼,圖中線段AB表示站立在廣場上的小亮,線段PO表示直立在廣場上的燈桿,點P表示照明燈
晚上,小亮在廣場乘涼,圖中線段AB表示站立在廣場上的小亮,線段PO表示直立在廣場上的燈桿,點P表示照明燈查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com