
 ,位于O點的正上方
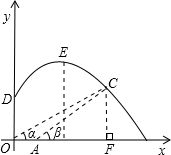
,位于O點的正上方 千米D點處的直升飛機向目標C發射防空導彈,該導彈運行達到距地面最大3千米時,相應水平距離為4千米.(即圖中E點)
千米D點處的直升飛機向目標C發射防空導彈,該導彈運行達到距地面最大3千米時,相應水平距離為4千米.(即圖中E點)
 )代入得,a=-
)代入得,a=- .
. (x-4)2+3
(x-4)2+3 x2+
x2+ x+
x+ .
.
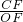 .
. ,
, =
=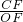 ,
, CF.
CF. ,
,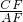 =
= ,∴AF=
,∴AF= CF.
CF. CF-
CF- CF=1,
CF=1, ,OF=
,OF= CF=
CF= ×
× =7,
=7, ).
). x2+
x2+ x+
x+ .
. .
. ),這頂點式,可求拋物線解析式;
),這頂點式,可求拋物線解析式;

科目:初中數學 來源: 題型:解答題
 選轉后的圖形中有多少個等腰直角三角形.
選轉后的圖形中有多少個等腰直角三角形.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
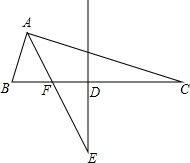 如圖,△ABC中,∠BAC=90°,BC的垂直平分線和BC相交于點D,和∠BAC的平分線AE相交于點E,AE和BC相交于點F.求證:DE=
如圖,△ABC中,∠BAC=90°,BC的垂直平分線和BC相交于點D,和∠BAC的平分線AE相交于點E,AE和BC相交于點F.求證:DE= BC.
BC.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com