Question

2．已知：拋物線y=x²+2（k+1）x+k²+2k．
（1）求證：無論k取任何實數，拋物線與x軸總有兩個交點；
（2）設拋物線頂點為C，與x軸交于A，B兩點，點A在點B的左邊，求證：無論k取任何實數，△ABC的面積總為確定的值．

Answer 1

分析 （1）根據原式等于0，利用根的判別式△＞0即可得出答案；
（2）根據拋物線解析式求得電費A、B、C的坐標，利用三角形的面積公式可以求得△ABC的面積．

解答 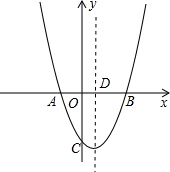（1）解：令y=0，則x²+2（k+1）x+k²+2k=0，
∴△=4（k+1）²-4（k²+2k）=4＞0，
∴無論k取任何實數，拋物線與x軸總有兩個交點．

（2）證明：解方程 x²+2（k+1）x+k²+2k=0，
得 x=-k，或x=-k-2．
∴A（-k-2，0），B（-k，0）．
∴AB=2．
∴AB的中點D（-k-1，0）．
當x=-k-1時，y=-1．
∴點C的縱坐標y_c=-1．
∴S_△ABC=$\frac{1}{2}$AB×|y_c|=1．
∴無論k取任何實數，△ABC的面積總為確定的值．

點評 本題考查了二次函數y=ax²+bx+c的交點與一元二次方程ax²+bx+c=0根之間的關系，拋物線與坐標軸交點坐標的求法，三角形的面積，難度適中．