日韩在线不卡,91社区在线观看高清,www.久久.com

精英家教網 > 初中數學 > 題目詳情

等式的性質1：等式的兩邊都加上(或都減去)同一個數或式，所得結果仍是________；

等式的性質2：等式的兩邊同乘以(或都除以)同一個不為零的數或式，所得結果仍是________．

答案：等式;等式

練習冊系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：初中數學 來源： 題型：

10、情景再現：
利用等式的性質解下列方程
（1）x+1=6（2）3-x=7
解：（1）方程兩邊都同時減去1，得：
x+1-1=6-1 x=6-1 x=5
（2）方程兩邊都加上x得
3-x+x=7+x 3=7+x
方程兩邊都減去7得
3-7=7+x-7
∴-4=x
習慣上寫成：x=-4
觀察上面解的過程實際是把原方程中已知項“+1”，改變符號后從方程左邊移到了右邊．這種變形叫做移項．
觀察并思考第（2）小題中有哪一項被移項了：

x、7

．
利用移項解下列方程
（1）x-5=11 （2）3=11-x
解：移項得

x=11+5

解：移項得

x=11-3

∴x=

x=16

∴

x=8

∴x=

查看答案和解析>>

科目：初中數學 來源： 題型：

20、如圖，在△ABC中，∠ACB=90°，CD⊥AB，垂足為D，∠BCD=35°，
求：（1）∠EBC的度數；（2）∠A的度數．
對于上述問題，在以下解答過程的空白處填上適當的內容（理由或數學式）．
解：（1）∵CD⊥AB（已知）
∴∠CDB=

90°

∵∠EBC=∠CDB+∠BCD

三角形的外角等于與它不相鄰兩個內角的和

∴∠EBC=

90°

+35°=

125°

．（等量代換）
（2）∵∠EBC=∠A+ACB

三角形的外角等于與它不相鄰兩個內角的和

∴∠A=∠EBC-∠ACB．（等式的性質）
∵∠ACB=90°（已知）
∴∠A=

125°

-90°=

35°

．（等量代換）

查看答案和解析>>

科目：初中數學 來源： 題型：閱讀理解

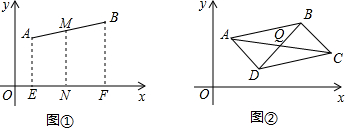讓我們一起來探索平面直角坐標系中平行四邊形的頂點的坐標之間的關系．
第一步：數軸上兩點連線的中點表示的數．自己畫一個數軸，如果點A、B分別表示-2、4，則線段AB的中點M表示的數是

．再試幾個，我們發現：數軸上連接兩點的線段的中點所表示的數是這兩點所表示數的平均數．
第二步；平面直角坐標系中兩點連線的中點的坐標（如圖①）為便于探索，我們在第一象限內取兩點A（x₁，y₁），B（x₂，y₂），取線段AB的中點M，分別作A、B到x軸的垂線段AE、BF，取EF的中點N，則MN是梯形AEFB的中位線，故MN⊥x軸，利用第一步的結論及梯形中位線的性質，我們可以得到點M的坐標是（

x1+x2

，

y1+y2

）（用x₁，y₁，x₂，y₂表示），AEFB是矩形時也可以．我們的結論是：平面直角坐標系中連接兩點的線段的中點的橫（縱）坐標等于這兩點的橫（縱）坐標的平均數．
第三步：平面直角坐標系中平行四邊形的頂點坐標之間的關系（如圖②）在平面直角坐標系中畫一個平行四邊形ABCD，設A（x₁，y₁），B（x₂，y₂），C（x₃，y₃），D（x₄，y₄），則其對角線交點Q的坐標可以表示為Q（

x1+x3

，

y1+y3

），也可以表示為Q（

x2+x4

，

y2+y4

），經過比較，我們可以分別得出關于x₁，x₂，x₃，x₄及，y₁，y₂，y₃，y₄的兩個等式是

x₁+x₃=x₂+x₄

和

y₁+y₃=y₂+y₄

．我們的結論是：平面直角坐標系中平行四邊形的對角頂點的橫（縱）坐標的

和相等

．

查看答案和解析>>

科目：初中數學 來源： 題型：閱讀理解

閱讀小明解方程的過程回答問題．
解方程：2x+9=3（x+2）
步驟①2x+9=3x+6
步驟②2x-6=3x-9
步驟③2（x-3）=3（x-3）
步驟④2-3
（1）上述變形中，由步驟①到步驟②變形的依據是

等式的基本性質或移項法則

．
（2）你認為上述變形正確嗎，如果不正確請指出錯誤的步驟，并說明不正確的理由．

查看答案和解析>>

科目：初中數學 來源： 題型：

讓我們一起來探索平面直角坐標系中平行四邊形的頂點的坐標之間的關系。
第一步：數軸上兩點連線的中點表示的數
自己畫一個數軸，如果點A、B分別表示-2、4，則線段AB的中點M表示的數是。再試幾個，我們發現：
數軸上連結兩點的線段的中點所表示的數是這兩點所表示數的平均數。
第二步；平面直角坐標系中兩點連線的中點的坐標（如圖①）
為便于探索，我們在第一象限內取兩點A（x₁,y₁），B（x₂,y₂）,取線段AB的中點M，分別作A、B到x軸的垂線段AE、BF，取EF的中點N，則MN是梯形AEFB的中位線，故MN⊥x軸，利用第一步的結論及梯形中位線的性質，我們可以得到點M的坐標是（，）（用x₁,y₁，x₂,y₂表示），AEFB是矩形時也可以。我們的結論是：平面直角坐標系中連結兩點的線段的中點的橫（縱）坐標等于這兩點的橫（縱）坐標的平均數。

圖① 圖②
第三步：平面直角坐標系中平行四邊形的頂點坐標之間的關系（如圖②）
在平面直角坐標系中畫一個平行四邊形ABCD，設A（x₁,y₁），B（x₂,y₂），C（x₃,y₃）,
D（x₄,y₄）,則其對角線交點Q的坐標可以表示為Q（，），也可以表示為Q（，），經過比較，我們可以分別得出關于x₁,x₂,x₃,x₄及,y₁,y₂,y₃,y₄的兩個等式是和。我們的結論是：平面直角坐標系中平行四邊形的對角頂點的橫（縱）坐標的。

查看答案和解析>>

同步練習冊答案

日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

練習冊

高中

初中

小學