
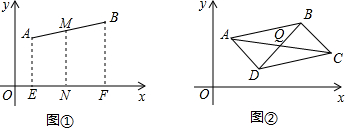 讓我們一起來探索平面直角坐標系中平行四邊形的頂點的坐標之間的關系.
讓我們一起來探索平面直角坐標系中平行四邊形的頂點的坐標之間的關系.| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
| y1+y2 |
| 2 |
| x1+x3 |
| 2 |
| x1+x3 |
| 2 |
| y1+y3 |
| 2 |
| y1+y3 |
| 2 |
| x2+x4 |
| 2 |
| x2+x4 |
| 2 |
| y2+y4 |
| 2 |
| y2+y4 |
| 2 |
 .
.| x1+x2 |
| 2 |
| AE+BF |
| 2 |
| y1+y2 |
| 2 |
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
| x1+x3 |
| 2 |
| y1+y3 |
| 2 |
| x2+x4 |
| 2 |
| y2+y4 |
| 2 |
| x1+x3 |
| 2 |
| y1+y3 |
| 2 |
| x2+x4 |
| 2 |
| y2+y4 |
| 2 |


科目:初中數學 來源: 題型:
讓我們一起來探索平面直角坐標系中平行四邊形的頂點的坐標之間的關系。
第一步:數軸上兩點連線的中點表示的數
自己畫一個數軸,如果點A、B分別表示-2、4,則線段AB的中點M表示的數是 。 再試幾個,我們發現:
數軸上連結兩點的線段的中點所表示的數是這兩點所表示數的平均數。
第二步;平面直角坐標系中兩點連線的中點的坐標(如圖①)
為便于探索,我們在第一象限內取兩點A(x1,y1),B(x2,y2),取線段AB的中點M,分別作A、B到x軸的垂線段AE、BF,取EF的中點N,則MN是梯形AEFB的中位線,故MN⊥x軸,利用第一步的結論及梯形中位線的性質,我們可以得到點M的坐標是( , )(用x1,y1,x2,y2表示),AEFB是矩形時也可以。我們的結論是:平面直角坐標系中連結兩點的線段的中點的橫(縱)坐標等于這兩點的橫(縱)坐標的平均數。

圖① 圖②
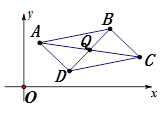
第三步:平面直角坐標系中平行四邊形的頂點坐標之間的關系(如圖②)
在平面直角坐標系中畫一個平行四邊形ABCD,設A(x1,y1),B(x2,y2),C(x3,y3),
D(x4,y4),則其對角線交點Q的坐標可以表示為Q( , ),也可以表示為Q( , ),經過比較,我們可以分別得出關于x1,x2,x3,x4及,y1,y2,y3,y4的兩個等式是 和 。 我們的結論是:平面直角坐標系中平行四邊形的對角頂點的橫(縱)坐標的 。
查看答案和解析>>
科目:初中數學 來源: 題型:


查看答案和解析>>
科目:初中數學 來源:2011-2012學年江蘇省呂良中學八年級第一學期第二次階段檢測數學卷.doc 題型:解答題
讓我們一起來探索平面直角坐標系中平行四邊形的頂點的坐標之間的關系。
第一步:數軸上兩點連線的中點表示的數
自己畫一個數軸,如果點A、B分別表示-2、4,則線段AB的中點M表示的數是 。 再試幾個,我們發現:
數軸上連結兩點的線段的中點所表示的數是這兩點所表示數的平均數。
第二步;平面直角坐標系中兩點連線的中點的坐標(如圖①)
為便于探索,我們在第一象限內取兩點A(x1,y1),B(x2,y2),取線段AB的中點M,分別作A、B到x軸的垂線段AE、BF,取EF的中點N,則MN是梯形AEFB的中位線,故MN⊥x軸,利用第一步的結論及梯形中位線的性質,我們可以得到點M的坐標是( , )(用x1,y1,x2,y2表示),AEFB是矩形時也可以。我們的結論是:平面直角坐標系中連結兩點的線段的中點的橫(縱)坐標等于這兩點的橫(縱)坐標的平均數。

圖① 圖②
第三步:平面直角坐標系中平行四邊形的頂點坐標之間的關系(如圖②)
在平面直角坐標系中畫一個平行四邊形ABCD,設A(x1,y1),B(x2,y2),C(x3,y3),
D(x4,y4),則其對角線交點Q的坐標可以表示為Q( , ),也可以表示為Q( , ),經過比較,我們可以分別得出關于x1,x2,x3,x4及,y1,y2,y3,y4的兩個等式是 和 。 我們的結論是:平面直角坐標系中平行四邊形的對角頂點的橫(縱)坐標的 。
查看答案和解析>>
科目:初中數學 來源:2013屆江蘇省八年級第一學期第二次階段檢測數學卷 題型:選擇題
讓我們一起來探索平面直角坐標系中平行四邊形的頂點的坐標之間的關系。
第一步:數軸上兩點連線的中點表示的數
自己畫一個數軸,如果點A、B分別表示-2、4,則線段AB的中點M表示的數是 。 再試幾個,我們發現:
數軸上連結兩點的線段的中點所表示的數是這兩點所表示數的平均數。
第二步;平面直角坐標系中兩點連線的中點的坐標(如圖①)
為便于探索,我們在第一象限內取兩點A(x1,y1),B(x2,y2),取線段AB的中點M,分別作A、B到x軸的垂線段AE、BF,取EF的中點N,則MN是梯形AEFB的中位線,故MN⊥x軸,利用第一步的結論及梯形中位線的性質,我們可以得到點M的坐標是( , )(用x1,y1,x2,y2表示),AEFB是矩形時也可以。我們的結論是:平面直角坐標系中連結兩點的線段的中點的橫(縱)坐標等于這兩點的橫(縱)坐標的平均數。


圖① 圖②
第三步:平面直角坐標系中平行四邊形的頂點坐標之間的關系(如圖②)
在平面直角坐標系中畫一個平行四邊形ABCD,設A(x1,y1),B(x2,y2),C(x3,y3),
D(x4,y4),則其對角線交點Q的坐標可以表示為Q( , ),也可以表示為Q( , ),經過比較,我們可以分別得出關于x1,x2,x3,x4及,y1,y2,y3,y4的兩個等式是 和 。 我們的結論是:平面直角坐標系中平行四邊形的對角頂點的橫(縱)坐標的 。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com