
分析 (1)(2)代入計算即可求解;
(3)根據乘法分配律即可證明:an+1-an=an-1(n≥2);
(4)根據(3)的關系可求斐波那契數列中的前8個數.
解答 解:(1)a1=$\frac{1}{\sqrt{5}}$[($\frac{1+\sqrt{5}}{2}$)-($\frac{1-\sqrt{5}}{2}$)]=$\frac{1}{\sqrt{5}}$×$\sqrt{5}$=1;
(2)a2=$\frac{1}{\sqrt{5}}$[($\frac{1+\sqrt{5}}{2}$)2-($\frac{1-\sqrt{5}}{2}$)2]=$\frac{1}{\sqrt{5}}$×$\sqrt{5}$=1;
(3)證明:an+1-an=$\frac{1}{\sqrt{5}}$[($\frac{1+\sqrt{5}}{2}$)n+1-($\frac{1-\sqrt{5}}{2}$)n+1]-$\frac{1}{\sqrt{5}}$[($\frac{1+\sqrt{5}}{2}$)n-($\frac{1-\sqrt{5}}{2}$)n]
=$\frac{1}{\sqrt{5}}$[($\frac{1+\sqrt{5}}{2}$)n+1-($\frac{1+\sqrt{5}}{2}$)n]-$\frac{1}{\sqrt{5}}$[($\frac{1-\sqrt{5}}{2}$)n+1-($\frac{1-\sqrt{5}}{2}$)n]
=$\frac{1}{\sqrt{5}}$[($\frac{1+\sqrt{5}}{2}$)n($\frac{1+\sqrt{5}}{2}$-1)]-$\frac{1}{\sqrt{5}}$[($\frac{1-\sqrt{5}}{2}$)n($\frac{1-\sqrt{5}}{2}$-1)]
=$\frac{1}{\sqrt{5}}$[($\frac{1+\sqrt{5}}{2}$)n($\frac{\sqrt{5}-1}{2}$)]-$\frac{1}{\sqrt{5}}$[($\frac{1-\sqrt{5}}{2}$)n(-$\frac{1+\sqrt{5}}{2}$)]
=$\frac{1}{\sqrt{5}}$[($\frac{1+\sqrt{5}}{2}$)n-1-($\frac{1-\sqrt{5}}{2}$)n-1];
(4)斐波那契數列中的前8個數是1,1,2,3,5,8,13,21.
點評 此題考查了二次根式的應用,關鍵是熟悉斐波那契數列的規律.


 新非凡教輔沖刺100分系列答案
新非凡教輔沖刺100分系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{1}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{5}{6}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖△PAB中,PA=PB,PB為⊙O的切線,B為切點,連接OP交AB于點C,延長BO與⊙O交于點D、與PA的延長線交于點E
如圖△PAB中,PA=PB,PB為⊙O的切線,B為切點,連接OP交AB于點C,延長BO與⊙O交于點D、與PA的延長線交于點E查看答案和解析>>
科目:初中數學 來源: 題型:解答題
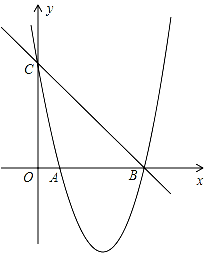 如圖,已知拋物線y=x2+bx+c的圖象與x軸的一個交點為B(5,0),另一個交點為A,且與y軸交于點C(0,5).
如圖,已知拋物線y=x2+bx+c的圖象與x軸的一個交點為B(5,0),另一個交點為A,且與y軸交于點C(0,5).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com