
 如圖,有一塊四邊形形狀的鐵皮ABCD,BC=CD=6,AB=2AD,∠ABC=∠ADB=90°,以C為圓心,CB為半徑作弧BD得一扇形CBD,剪下扇形并用它圍成一圓錐的側面.
如圖,有一塊四邊形形狀的鐵皮ABCD,BC=CD=6,AB=2AD,∠ABC=∠ADB=90°,以C為圓心,CB為半徑作弧BD得一扇形CBD,剪下扇形并用它圍成一圓錐的側面.分析 (1)由已知條件可得∠DBC=30°,所以∠DBC=60°,則△CDB為等邊三角形,進而求出∠C的度數;
(2)利用弧長公式可以求出弧BD的長,即圓錐底面圓的周長,從而求出圓的半徑.
解答 解:(1)∵∠ABC=90°,AB=2AD,
∴sin∠ABD=$\frac{AD}{AB}$=$\frac{1}{2}$,
∴∠ABD=30°,
∵∠ADB=90°,
∴∠DBC=90°-30°=60°,
∵BC=CD=6,
∴△CBD是等邊三角形,
∴∠BCD=60°;
(2)∵${l}_{\widehat{BD}}$=$\frac{60π×12}{180}$=2π,
∴2π=2πr,
∴r=1.
點評 本題考查了直角三角形的性質、等邊三角形的判定和等邊三角形的性質以及考查有關扇形和圓錐的相關計算.解題思路:解決此類問題時要緊緊抓住兩者之間的兩個對應關系:(1)圓錐的母線長等于側面展開圖的扇形半徑;(2)圓錐的底面周長等于側面展開圖的扇形弧長.正確對這兩個關系的記憶是解題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
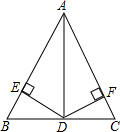 如圖,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于點E,DF⊥AC于點F.
如圖,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于點E,DF⊥AC于點F.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 3.0037×1013元 | B. | 3.00×1013元 | C. | 30.1×1012元 | D. | 3.01×1013元 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com