
 已知:如圖所示,直線l的解析式為y=$\frac{3}{4}$x-3,并且與x軸、y軸分別交于點A、B.
已知:如圖所示,直線l的解析式為y=$\frac{3}{4}$x-3,并且與x軸、y軸分別交于點A、B.分析 (1)對于直線y=$\frac{3}{4}$x-3,令x=0,得y=-3,令y=0得,x=4,可得A、B兩點坐標.
(2)設經過ts后點A在⊙P上,根據PA=1列出方程即可解決問題,注意兩解.
(3))⊙P可以經過B點,理由如下:設t秒后點B在⊙P上,t秒后點P坐標(4t,0),⊙P的半徑為1+6t,由題意,PB2=OB2+OP2,可得方程32+(4t)2=(1+6t)2,解方程即可.
解答 解:(1)對于直線y=$\frac{3}{4}$x-3,令x=0,得y=-3,令y=0得,x=4,
∴A(4,0),B(0,-3).
(2)設經過ts后點A在⊙P上,
∵⊙P的半徑為1,
∴PA=1時,點A在⊙P上,
∴P(3,0)或(5,0),
∴4-4t=1或4t-4=1時點A在⊙P上
∴t=$\frac{3}{4}$s或$\frac{5}{4}$s時,點A在⊙P上.
(3)⊙P可以經過B點,理由如下:
設t秒后點B在⊙P上,∵t秒后點P坐標(4t,0),⊙P的半徑為1+6t,
由題意,PB2=OB2+OP2,
∴32+(4t)2=(1+6t)2,
整理得5t2+3t-2=0,解得t=$\frac{2}{5}$或-1(舍棄),
∴t=$\frac{2}{5}$時,⊙P經過點B.
點評 本題考查圓綜合題,點與圓位置關系,一元一次方程等知識,解題的關鍵是靈活運用所學知識解決問題,學會用方程的思想思考問題,屬于中考常考題型.


 學業測評一課一測系列答案
學業測評一課一測系列答案科目:初中數學 來源: 題型:選擇題
| A. | 0個 | B. | 1個 | C. | 2個 | D. | 3個 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知:如圖,在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=16,BC=18.連接BD,AE⊥BD,垂足為點E.
已知:如圖,在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=16,BC=18.連接BD,AE⊥BD,垂足為點E.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
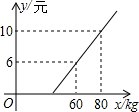 某地長途汽車客運公司規定每位旅客可隨身攜帶一定的行李,如果超出規定,那么需要購買行李票,行李票 y(元)是行李質量 x(kg)的一次函數,其圖象如圖.
某地長途汽車客運公司規定每位旅客可隨身攜帶一定的行李,如果超出規定,那么需要購買行李票,行李票 y(元)是行李質量 x(kg)的一次函數,其圖象如圖.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com