
如圖,在平面直角坐標系 中,直線
中,直線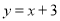 交x軸于A點,交y軸于B點,過A、B兩點的拋物線
交x軸于A點,交y軸于B點,過A、B兩點的拋物線 交
交 軸于另一點C,點D是拋物線的頂點.
軸于另一點C,點D是拋物線的頂點.

(1)求此拋物線的解析式.
(2)點P是直線AB上方的拋物線上一點,(不與點A、B重合),過點P作 軸的垂線交
軸的垂線交 軸于點H,交直線AB于點F,作PG⊥AB于點G,若△PFG的周長最大,求P點的坐標
軸于點H,交直線AB于點F,作PG⊥AB于點G,若△PFG的周長最大,求P點的坐標
(3)在拋物線 上是否存在除點D以外的點M,使得△ABM與△ABD的面積相等? 若存在,請求出此時點M的坐標,若不存在,請說明理由.
上是否存在除點D以外的點M,使得△ABM與△ABD的面積相等? 若存在,請求出此時點M的坐標,若不存在,請說明理由. 
(1) ;(2)P(
;(2)P( ,
, );(3)M1(﹣2,3),M2(
);(3)M1(﹣2,3),M2( ,
, ),M3(
),M3( ,
, ).
).
【解析】
試題分析:(1)將已知點的坐標代入二次函數的解析式利用待定系數法確定二次函數的解析式即可;
(2)首先根據△PFG是等腰直角三角形,設P( ,
, )得到F(
)得到F( ,
, ),進而得到PF=
),進而得到PF=
 ,從而得到△PFG周長為:
,從而得到△PFG周長為: ,配方后即可確定點P的坐標;
,配方后即可確定點P的坐標;
(3)當DM1∥AB,M3M2∥AB,且與AB距離相等時,根據同底等高可以確定△ABM與△ABD的面積相等,分別求得直線DM1解析式為: 和直線M3M2解析式為:
和直線M3M2解析式為: ,聯立之后求得交點坐標即可.
,聯立之后求得交點坐標即可.
試題解析:(1)∵直線AB: 與坐標軸交于A(﹣3,0)、B(0,3),
與坐標軸交于A(﹣3,0)、B(0,3),
代入拋物線解析式 中,得:
中,得: ,解得:
,解得: ,
,
∴拋物線解析式為: ;
;
(2)∵由題意可知△PFG是等腰直角三角形,設P( ,
, ),∴F(
),∴F( ,
, ),
),
∴PF=
 ,
,
△PFG周長為: =
= ,
,
∴當 時,△PFG周長的最大值,而當
時,△PFG周長的最大值,而當 時,
時, ,∴P(
,∴P( ,
, );
);
(3)點M有三個位置,如圖所示的M1、M2、M3,都能使△ABM的面積等于△ABD的面積.
此時DM1∥AB,M3M2∥AB,且與AB距離相等,
∵D(﹣1,4),∴E(﹣1,2)、則N(﹣1,0)
∵ 中,k=1,∴直線DM1解析式為:
中,k=1,∴直線DM1解析式為: ,直線M3M2解析式為:
,直線M3M2解析式為: ,
,
∴ 或
或 ,
,
∴ ,
, ,
, ,
, ,
,
∴M1(﹣2,3),M2( ,
, ),M3(
),M3( ,
, ).
).

考點:二次函數綜合題.


科目:初中數學 來源:2014-2015學年重慶市等五校九年級上學期期中聯考數學試卷(解析版) 題型:選擇題
下列五個命題:
(1)若直角三角形的兩條邊長為5和12,則第三邊長是13,
(2)如果a≥0,那么 ,
,
(3)若點P 在第三象限,則將點P繞原點順時針旋轉90º得P
在第三象限,則將點P繞原點順時針旋轉90º得P
 ,
,
(4)對角線互相垂直且相等的四邊形是正方形,
(5)某校初三(2)有7名同學的體能測試成績(單位:分)如下:50,48,47,50,48,49,48.這組數據的中位數和眾數是分別48,50,
其中不正確命題的個數是( )
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:初中數學 來源:2014-2015學年重慶市沙坪壩區九年級上學期期中聯考數學試卷(解析版) 題型:選擇題
如圖,AB/∥CD,∠C=800,∠CAD=600,則∠BAD的度數等于( )
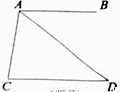
A.500 B.600 C.700 D.400
查看答案和解析>>
科目:初中數學 來源:2014-2015學年重慶市校七年級12月月考數學試卷(解析版) 題型:選擇題
如圖所示,關于線段、射線和直線的條數,下列說法正確的是( )

A.五條線段,三條射線
B.一條直線,三條線段
C.三條線段,兩條射線,一條直線
D.三條線段,三條射線
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com