
 如圖,O為Rt△ABC的直角邊AC上一點,以O(shè)C為半徑的半圓與斜邊AB相切于點D,交AC于點E,已知AB=5,AC=4,求BD的長和⊙O的半徑.
如圖,O為Rt△ABC的直角邊AC上一點,以O(shè)C為半徑的半圓與斜邊AB相切于點D,交AC于點E,已知AB=5,AC=4,求BD的長和⊙O的半徑. 分析 在直角△ABC中利用勾股定理求得BC的長,然后證明BC是切線,利用切線長定理求得BD的長,然后連接OD,證明△OAD∽△BAC,利用相似三角形的對應(yīng)邊的比相等求解.
解答 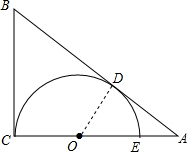 解:在直角△ABC中,BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
解:在直角△ABC中,BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∵∠ACB=90°,即BC⊥AC,
∴BC是半圓的切線,
又∵AB與半圓相切,
∴BD=BC=3,AD=AB-BD=5-3=2.
連接OD.
∵AB是切線,
∴OD⊥AB,
∴∠ODA=∠BCA,
又∵∠A=∠A,
∴△OAD∽△BAC,
∴$\frac{OD}{BC}$=$\frac{AD}{AC}$,即$\frac{OD}{3}$=$\frac{2}{4}$,
解得OD=$\frac{3}{2}$.即半徑長是$\frac{3}{2}$.
點評 本題考查了勾股定理、切線的判定與性質(zhì)以及相似三角形的判定與性質(zhì),正確證明△OAD∽△BAC是關(guān)鍵.


 孟建平小學滾動測試系列答案
孟建平小學滾動測試系列答案科目:初中數(shù)學 來源: 題型:選擇題
| A. | 15噸 | B. | 12$\frac{1}{5}$噸 | C. | 15$\frac{1}{5}$噸 | D. | 3$\frac{1}{5}$噸 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
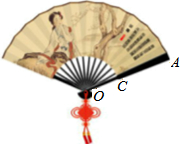 中國扇文化有著深厚的文化底蘊,是民族文化的一個組成部分,它與竹文化、佛教文化有著密切關(guān)系.歷來中國被譽為制扇王國.扇子主要材料是:竹、木、紙、象牙、玳瑁、翡翠、飛禽翎毛、其它棕櫚葉、檳榔葉、麥桿、蒲草等也能編制成各種千姿百態(tài)的日用工藝扇,造型優(yōu)美,構(gòu)造精制,經(jīng)能工巧匠精心鏤、雕、燙、鉆或名人揮毫題詩作畫,使扇子藝術(shù)身價倍增.折扇,古稱“聚頭扇“,或稱為撒扇,或折疊扇,以其收攏時能夠二頭合并歸一而得名.如圖,折扇的骨柄OA的長為5a,扇面的寬CA的長為3a,折扇張開的角度為n°,求出扇面的面積(用代數(shù)式表示).
中國扇文化有著深厚的文化底蘊,是民族文化的一個組成部分,它與竹文化、佛教文化有著密切關(guān)系.歷來中國被譽為制扇王國.扇子主要材料是:竹、木、紙、象牙、玳瑁、翡翠、飛禽翎毛、其它棕櫚葉、檳榔葉、麥桿、蒲草等也能編制成各種千姿百態(tài)的日用工藝扇,造型優(yōu)美,構(gòu)造精制,經(jīng)能工巧匠精心鏤、雕、燙、鉆或名人揮毫題詩作畫,使扇子藝術(shù)身價倍增.折扇,古稱“聚頭扇“,或稱為撒扇,或折疊扇,以其收攏時能夠二頭合并歸一而得名.如圖,折扇的骨柄OA的長為5a,扇面的寬CA的長為3a,折扇張開的角度為n°,求出扇面的面積(用代數(shù)式表示).查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
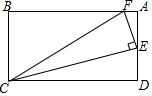 已知,如圖,在矩形ABC中.E是AD的中點,EF⊥EC交AB于點F,連FC(AB>AE),求證:$\frac{DE}{AB}$=$\frac{AF}{DE}$.
已知,如圖,在矩形ABC中.E是AD的中點,EF⊥EC交AB于點F,連FC(AB>AE),求證:$\frac{DE}{AB}$=$\frac{AF}{DE}$.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
| 4 | 6 | 8 | 10 | … | 2n | … |
| 3 | 8 | 15 | 24 | … | … | |
| 5 | 10 | 17 | 26 | … | … |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com