
 如圖,直線L上有三個正方形a,b,c,若a,c的面積分別為1和9,則b的面積為( )
如圖,直線L上有三個正方形a,b,c,若a,c的面積分別為1和9,則b的面積為( )| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
分析 運(yùn)用正方形邊長相等,再根據(jù)同角的余角相等可得∠BAC=∠DCE,然后證明△ACB≌△DCE,再結(jié)合全等三角形的性質(zhì)和勾股定理來求解即可.
解答 解:由于a、b、c都是正方形,所以AC=CD,∠ACD=90°;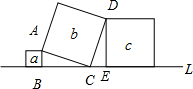
∵∠ACB+∠DCE=∠ACB+∠BAC=90°,即∠BAC=∠DCE,
在△ABC和△CED中,
$\left\{\begin{array}{l}{∠ABC=∠DEC=90°}\\{∠ACB=∠CDE}\\{AC=DC}\end{array}\right.$,
∴△ACB≌△DCE(AAS),
∴AB=CE,BC=DE;
在Rt△ABC中,由勾股定理得:AC2=AB2+BC2=AB2+DE2,
即Sb=Sa+Sc=1+9=10,
∴b的面積為10,
故選C.
點(diǎn)評 此題主要考查對全等三角形和勾股定理的綜合運(yùn)用,關(guān)鍵是證明△ACB≌△DCE.


 各地期末復(fù)習(xí)特訓(xùn)卷系列答案
各地期末復(fù)習(xí)特訓(xùn)卷系列答案 小博士期末闖關(guān)100分系列答案
小博士期末闖關(guān)100分系列答案 名校名師培優(yōu)作業(yè)本加核心試卷系列答案
名校名師培優(yōu)作業(yè)本加核心試卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 明天太陽從西邊升起 | |
| B. | 擲出一枚硬幣,正面朝上 | |
| C. | 打開電視機(jī),正在播放“新聞聯(lián)播” | |
| D. | 任意畫一個三角形,它的內(nèi)角和等于180° |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 3x+2y=7 | B. | 3x2-2x=1 | C. | x-2=3 | D. | x-1=$\frac{1}{x}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | a<2 | B. | a=2 | C. | a>2 | D. | a≤2 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com