
【題目】以四邊形![]() 的邊
的邊![]() 、
、![]() 、
、![]() 、
、![]() 為斜邊分別向外側作等腰直角三角形,直角頂點分別為
為斜邊分別向外側作等腰直角三角形,直角頂點分別為![]() 、
、![]() 、
、![]() 、
、![]() ,順次連結這四個點,得四邊形
,順次連結這四個點,得四邊形![]() .
.
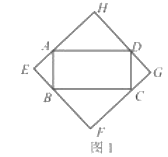
(1)如圖1,當四邊形![]() 為矩形時,請判斷四邊形
為矩形時,請判斷四邊形![]() 的形狀(不要求證明).
的形狀(不要求證明).
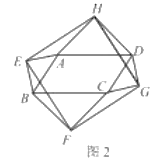
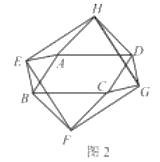
(2)如圖2,當四邊形![]() 為一般平行四邊形時,設
為一般平行四邊形時,設![]()
①試用含![]() 的代數式表示
的代數式表示![]() ,寫出解答過程;
,寫出解答過程;
②求證:![]() ,并判斷四邊形
,并判斷四邊形![]() 是什么四邊形?請說明理由.
是什么四邊形?請說明理由.
【答案】(1)四邊形![]() 是正方形;
是正方形;
(2)①![]() =90°+
=90°+![]() ,②HE=HG證明過程見詳解;
,②HE=HG證明過程見詳解;
四邊形![]() 是正方形,理由見詳解.
是正方形,理由見詳解.
【解析】
(1)根據等腰直角三角形的性質得到∠E=∠F=∠G=∠H=90°,求出四邊形是矩形,根據勾股定理求出AH=HD=![]() AD,DG=GC=
AD,DG=GC=![]() DC ,BF=CF=
DC ,BF=CF=![]() BC,EA=EB=
BC,EA=EB=![]() AB,推出EF=FG=GH=EH,根據正方形的判定推出四邊形EFGH是正方形即可;
AB,推出EF=FG=GH=EH,根據正方形的判定推出四邊形EFGH是正方形即可;
(2)①根據平行四邊形的性質得出,∠BAD=180°-![]() ,根據△HAD和△EAB是等腰直角三角形,得到∠HAD=∠EAB=45°,求出∠HAE即可;
,根據△HAD和△EAB是等腰直角三角形,得到∠HAD=∠EAB=45°,求出∠HAE即可;
②根據△AEB和△DGC是等腰直角三角形,得出AE=![]() AB,DG=
AB,DG=![]() CD,平行四邊形的性質得出AB=CD,求出∠HDG=90°+
CD,平行四邊形的性質得出AB=CD,求出∠HDG=90°+![]() =∠HAE,根據SAS證△HAE≌△HDG,根據全等三角形的性質即可得出HE=HG;同理可得GH=GF,FG=FE,推出GH=GF=EF=HE,得出菱形EFGH,根據∠AHD=90°得∠EHG=90°,即可推出結論.
=∠HAE,根據SAS證△HAE≌△HDG,根據全等三角形的性質即可得出HE=HG;同理可得GH=GF,FG=FE,推出GH=GF=EF=HE,得出菱形EFGH,根據∠AHD=90°得∠EHG=90°,即可推出結論.
解:(1)∵以矩形![]() 的邊
的邊![]() 、
、![]() 、
、![]() 、
、![]() 為斜邊分別向外側作等腰直角三角形,
為斜邊分別向外側作等腰直角三角形,
∴∠E=∠F=∠G=∠H=90°,∠HAD=∠EAB=45°,∠BAD=90°,
∴∠EAH=180°,即E、A、H三點在一條直線上,
同理可知:E、B、F三點共線,F、C、G三點共線,G、D、H三點共線,
∴AH=HD=![]() AD,DG=GC=
AD,DG=GC=![]() DC ,BF=CF=
DC ,BF=CF=![]() BC,EA=EB=
BC,EA=EB=![]() AB,
AB,
∴EF=FG=GH=EH,
∴四邊形EFGH是正方形.
(2)①∠HAE=90°+![]()
解:在平行四邊形ABCD中
AB//CD,
∴∠BAD=180°-∠ADC=180°-![]()
∵△HAD和△EAB是等腰直角三角形,
∴∠HAD=∠EAB=45°,
∴∠HAE=360°-∠HAD-∠EAB-∠BAD=360°-45°-45°-(180°-![]() )=90°+
)=90°+![]()
故用含![]() 的代數式表示∠HAE是90°+
的代數式表示∠HAE是90°+![]()
,
②證明:∵△AEB和△DGC是等腰直角三角形,
∴AE=![]() AB,DG=
AB,DG=![]() DC
DC
∵平行四邊形ABCD中,AB=CD,
∴AE=DG,
∵△AHD和△DGC是等腰直角三角形,
∴∠HDA=∠CDG=45°,
∴∠HDG=∠HDA+∠ADC+∠CDG=90°+![]() =∠HAE
=∠HAE
∵△AHD是等腰直角三角形
∴HA=HD
∴△HAE≌△HDG
∴HE=HG.
答:四邊形EFGH是正方形
理由是:
由以上同理可得:
GH=GF,FG=FE,
∵HE=HG,
∴GH=GF=EF=HE,
∴四邊形EFGH是菱形,
∵△HAE≌△HDG,
∴∠DHG=∠AHE,
∵∠AHD=∠AHG+∠DHG=90°
∴∠EHG=∠AHG+∠AHE=90°
∴四邊形EFGH是正方形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
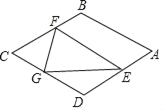
【題目】如圖,在菱形ABCD中,AB=![]() ,∠B=120°,點E是AD邊上的一個動點(不與A,D重合),EF∥AB交BC于點F,點G在CD上,DG=DE.若△EFG是等腰三角形,則DE的長為_____.
,∠B=120°,點E是AD邊上的一個動點(不與A,D重合),EF∥AB交BC于點F,點G在CD上,DG=DE.若△EFG是等腰三角形,則DE的長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1~4,在直角邊分別為3和4的直角三角形中,每多作一條斜邊上的高就增加一個三角形的內切圓,依此類推,圖10中有10個直角三角形的內切圓,它們的面積分別記為S1,S2,S3,…,S10,則S1+S2+S3+…+S10= .
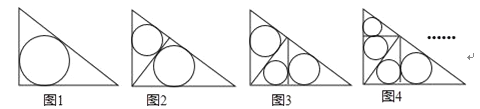
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】操作:將一把三角尺放在邊長為1的正方形ABCD上,并使它的直角頂點P在對角線AC上滑動,直角的一邊始終經過點B,另一邊與射線DC相交于點Q,設A、P兩點間的距離為x.
探究:
(1)當點Q在邊CD上時,線段PQ與線段PB之間有怎樣的大小關系?試證明你觀察到的結論;
(2)當點Q在邊CD上時,設四邊形PBCQ的面積為y,求y與x之間的函數關系式,并寫出x的取值范圍;(3)當點P在線段AC上滑動時,△PCQ是否能成為等腰三角形?如果可能,指出所有能使△PCQ成為等腰三角形的點Q的位置,并求出相應x的值;如果不可能,試說明理由.
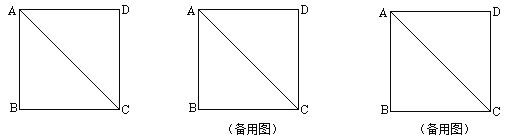
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,OA,OB是⊙O的兩條半徑,OA⊥OB,C是半徑OB上一動點,連結AC并延長交⊙O于D,過點D作圓的切線交OB的延長線于E,已知OA=8.
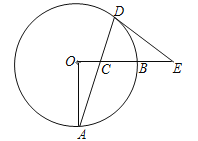
(1)求證:∠ECD=∠EDC;
(2)若tanA=![]() ,求DE長;
,求DE長;
(3)當∠A從15°增大到30°的過程中,求弦AD在圓內掃過的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店一周內甲、乙兩種計算器每天的銷售量如下(單位:個):
類別/星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 平均數 |
甲 |
|
|
|
|
|
|
| |
乙 |
|
|
|
|
|
|
|
|
(1)將表格填寫完整.
(2)求甲種計算器本周銷售量的方差.
(3)已知乙種計算器本周銷售量的方差為![]() ,本周哪種計算器的銷售量比較穩定?說明理由.
,本周哪種計算器的銷售量比較穩定?說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD邊長為3,連接AC,AE平分∠CAD,交BC的延長線于點E,FA⊥AE,交CB延長線于點F,則EF的長為__________.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com