
【題目】如圖,拋物線![]() 與x軸相交于A(3,0)、B兩點,與y軸交于點C(0,3),點B在x軸的負半軸上,且
與x軸相交于A(3,0)、B兩點,與y軸交于點C(0,3),點B在x軸的負半軸上,且![]() .
.

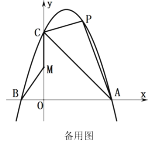
(1)求拋物線的函數(shù)關(guān)系式;
(2)若P是拋物線上且位于直線![]() 上方的一動點,求
上方的一動點,求![]() 的面積的最大值及此時點P的坐標(biāo);
的面積的最大值及此時點P的坐標(biāo);
(3)在線段![]() 上是否存在一點M,使
上是否存在一點M,使![]() 的值最小?若存在,請求出這個最小值及對應(yīng)的M點的坐標(biāo);若不存在,請說明理由.
的值最小?若存在,請求出這個最小值及對應(yīng)的M點的坐標(biāo);若不存在,請說明理由.
【答案】(1)![]() ;(2)
;(2)![]() 的面積的最大值為
的面積的最大值為![]() ,此時
,此時![]() ;(3)當(dāng)
;(3)當(dāng)![]() 時,
時,![]() 的最小值為
的最小值為![]() .
.
【解析】
(1)根據(jù)![]() 求出B點坐標(biāo),設(shè)交點式,用待定系數(shù)法即可求出函數(shù)關(guān)系式;
求出B點坐標(biāo),設(shè)交點式,用待定系數(shù)法即可求出函數(shù)關(guān)系式;
(2)作PD⊥x軸,與線段AC相交于D,根據(jù)![]() 表示
表示![]() 的面積,利用二次函數(shù)的性質(zhì)即可求出
的面積,利用二次函數(shù)的性質(zhì)即可求出![]() 的面積的最大值及此事P點坐標(biāo);
的面積的最大值及此事P點坐標(biāo);
(3)構(gòu)造CM為斜邊的等腰三角形,它的直角頂點為第一象限內(nèi)的N,可得出![]() =
=![]() 最小值即為BN.設(shè)
最小值即為BN.設(shè)![]() 可表示N點坐標(biāo),繼而可表示
可表示N點坐標(biāo),繼而可表示![]() ,利用二次函數(shù)的性質(zhì)即可求的
,利用二次函數(shù)的性質(zhì)即可求的![]() 最小值,以及此時M點坐標(biāo).
最小值,以及此時M點坐標(biāo).
解:(1)∵![]() ,
,![]()
∴OA=3,OB=1
∴![]()
∴設(shè)拋物線的交點式為![]() ,
,
將![]() 代入得
代入得![]() ,解得
,解得![]()
∴![]() ,
,
即該拋物線的函數(shù)關(guān)系式為![]() .
.
(2)作PD⊥x軸,與線段AC相交于D.
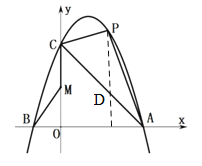
設(shè)直線AC:y=kx+d
將![]() ,
,![]() 分別代入
分別代入
得![]() ,解得
,解得![]() ,
,
所以y=-x+3.
設(shè)![]() ,則
,則![]() ,
,![]()
設(shè)△DCP以PD為底時高為h1,△DAP以PD為底時高為h2,則![]() 因為
因為![]() ,所以
,所以![]() 時取得最大值為
時取得最大值為![]() .
.![]() .
.
故![]() 的面積的最大值為
的面積的最大值為![]() ,此時
,此時![]() .
.
(3)存在,如下圖,作以CM為斜邊的等腰三角形,它的直角頂點為第一象限內(nèi)的N點,
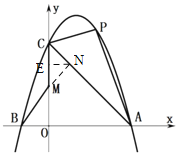
∵△MCN為等腰直角三角形,
∴MN=![]() ,即要使
,即要使![]() 最短,只需要
最短,只需要![]() 最短為BN即可,
最短為BN即可,
設(shè)![]() 則
則![]() ,
,![]()
∴![]()
當(dāng)![]() 時,
時,![]() 取得最小值為8,即
取得最小值為8,即![]() .
.
當(dāng)![]() 時,
時,![]() 的最小值為
的最小值為![]() .
.


 海淀黃岡名師導(dǎo)航系列答案
海淀黃岡名師導(dǎo)航系列答案 普通高中同步練習(xí)冊系列答案
普通高中同步練習(xí)冊系列答案科目:初中數(shù)學(xué) 來源: 題型:
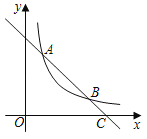
【題目】如圖,一次函數(shù)y=﹣x+3的圖象與反比例函數(shù)y=![]() (k≠0)在第一象限的圖象交于A(1,a)和B兩點,與x軸交于點C.
(k≠0)在第一象限的圖象交于A(1,a)和B兩點,與x軸交于點C.
(1)求反比例函數(shù)的解析式;
(2)若點P在x軸上,且△APC的面積為5,求點P的坐標(biāo);
(3)若點P在y軸上,是否存在點P,使△ABP是以AB為一直角邊的直角三角形?若存在,求出所有符合條件的P點坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
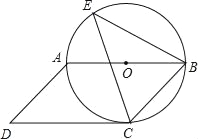
【題目】如圖,四邊形ABCD是平行四邊形,以邊AB為直徑的⊙O經(jīng)過點C,E是⊙O上的一點,且∠BEC=45°.
(1)試判斷CD與⊙O的位置關(guān)系,并說明理由;
(2)若BE=8cm,sin∠BCE=![]() ,求⊙O的半徑.
,求⊙O的半徑.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
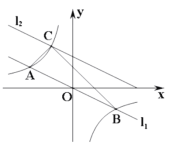
【題目】如圖,在平面直角坐標(biāo)系中,直線![]() 與反比例函數(shù)
與反比例函數(shù)![]() 的圖象交于A,B兩點(點A在點B左側(cè)),已知A點的縱坐標(biāo)是1:將直線
的圖象交于A,B兩點(點A在點B左側(cè)),已知A點的縱坐標(biāo)是1:將直線![]() 沿y向上平移后的直線
沿y向上平移后的直線![]() 與反比例函數(shù)
與反比例函數(shù)![]() 在第二象限內(nèi)交于點C,如果
在第二象限內(nèi)交于點C,如果![]() 的面積為3,則平移后的直線
的面積為3,則平移后的直線![]() 的函數(shù)表達式為_____.
的函數(shù)表達式為_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
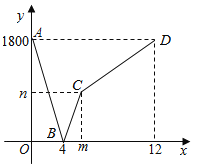
【題目】甲、乙兩地高速鐵路建設(shè)成功,一列動車從甲地開往乙地,一列普通列車從乙地開往甲地,兩車均勻速行駛并同時出發(fā),設(shè)普通列車行駛的時間為x(小時),兩車之間的距離為y(千米),圖中的折線表示y與x之間的函數(shù)關(guān)系,下列說法:
①甲、乙兩地相距1800千米;
②點B的實際意義是兩車出發(fā)后4小時相遇;
③m=6,n=900;
④動車的速度是450千米/小時.
其中不正確的是( )
A.①B.②C.③D.④
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線y=ax2+(1﹣2a)x+c(a,c是常數(shù),且a≠0),過點(0,2).
(1)求c的值,并通過計算說明點(2,4)是否也在該拋物線上;
(2)若該拋物線與直線y=5只有一個交點,求a的值;
(3)若當(dāng)0≤x≤2時,y隨x的增大而增大,求a的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系中,設(shè)二次函數(shù)![]() ,其中
,其中![]() .
.
(1)若函數(shù)![]() 的圖象經(jīng)過點
的圖象經(jīng)過點![]() ,求函數(shù)
,求函數(shù)![]() 的表達式;
的表達式;
(2)若一次函數(shù)![]() 的圖象與函數(shù)
的圖象與函數(shù)![]() 的圖象經(jīng)過
的圖象經(jīng)過![]() 軸上同一點,探究實數(shù)
軸上同一點,探究實數(shù)![]() 滿足的關(guān)系式;若
滿足的關(guān)系式;若![]() 隨
隨![]() 的變化能取得最大值,證明:當(dāng)
的變化能取得最大值,證明:當(dāng)![]() 取得最大值時,拋物線
取得最大值時,拋物線![]() 與
與![]() 軸只有一個交點;
軸只有一個交點;
(3)已知點![]() 和
和![]() 在函數(shù)
在函數(shù)![]() 的圖象上,若
的圖象上,若![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
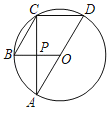
【題目】如圖,AD是⊙O的直徑,BC是弦,四邊形OBCD是平行四邊形,AC與OB相交于點P,給出下列結(jié)論:①AC⊥CD;②∠CAD=30°;③OB⊥AC;④CD=2OP.其中正確的個數(shù)為( )
A.4個B.3個C.2個D.1個
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com