
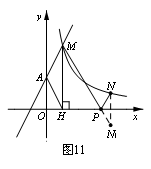
如圖11,直線![]() 與y軸交于A點,與反比例函數
與y軸交于A點,與反比例函數![]() (x>0)的圖象交
(x>0)的圖象交
于點M,過M作MH⊥x軸于點H,且tan∠AHO=2.
(1)求k的值;
(2)點N(a,1)是反比例函數![]() (x>0)圖像上的點,
(x>0)圖像上的點,
在x軸上是否存在點P,使得PM+PN最小,若存
在,求出點P的坐標;若不存在,請說明理由.
(1)由y=2x+2可知A(0,2),即OA=2.………………………………(1分)
∵tan∠AHO=2,∴OH=1.………………………………………………(2分)
∵MH⊥x軸,∴點M的橫坐標為1.
∵點M在直線y=2x+2上,
 ∴點M的縱坐標為4.即M(1,4).…………(3分)
∴點M的縱坐標為4.即M(1,4).…………(3分)
∵點M在y=![]() 上,∴k=1×4=4. …………(4分)
上,∴k=1×4=4. …………(4分)
(2)∵點N(a,1)在反比例函數![]() (x>0)上,
(x>0)上,
∴a=4.即點N的坐標為(4,1).…………(5分)
過N作N關于x軸的對稱點N1,連接MN1,交x軸于P(如圖11).
此時PM+PN最小. ………………………………………………(6分)
∵N與N1關于x軸的對稱,N點坐標為(4,1),
∴N1的坐標為(4,-1).……………………………………………………(7分)
設直線MN1的解析式為y=kx+b.
由![]() 解得k=-
解得k=-![]() ,b=
,b=![]() .…………………………………(9分)
.…………………………………(9分)
∴直線MN![]() 的解析式為
的解析式為![]() .
.
令y=0,得x=![]() . ∴P點坐標為(
. ∴P點坐標為(![]() ,0).………………………(10分)
,0).………………………(10分)


 世紀百通主體課堂小學課時同步達標系列答案
世紀百通主體課堂小學課時同步達標系列答案 世紀百通優練測系列答案
世紀百通優練測系列答案 百分學生作業本題練王系列答案
百分學生作業本題練王系列答案科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源:2010年高級中等學校招生全國統一考試數學卷(廣東深圳) 題型:解答題
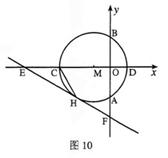
如圖10,以點M(-1,0)為圓心的圓與y軸、x軸分別交于點A、B、C、D,直線y=- x- 與⊙M相切于點H,交x軸于點E,交y軸于點F.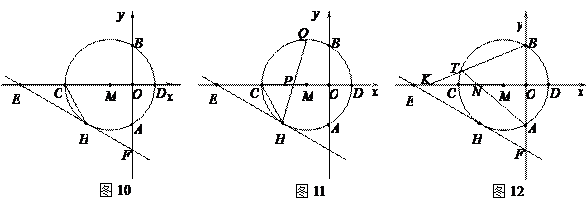
(1)請直接寫出OE、⊙M的半徑r、CH的長;(3分)
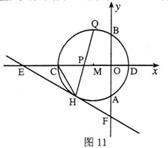
(2)如圖11,弦HQ交x軸于點P,且DP:PH=3:2,求cos∠QHC的值;(3分)
(3)如圖12,點K為線段EC上一動點(不與E、C重合),連接BK交⊙M于點T,弦AT交x軸于點N.是否存在一個常數a,始終滿足MN·MK=a,如果存在,請求出a的值;如果不存在,請說明理由.(3分)
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖10,以點M(—1,0)為圓心的圓與![]() 軸、
軸、![]() 軸分別交于點A、B、C、D,直線
軸分別交于點A、B、C、D,直線![]() 與⊙M相切于點H,交
與⊙M相切于點H,交![]() 軸于點E,求
軸于點E,求![]() 軸于點F。
軸于點F。
(1)請直接寫出OE、⊙M的半徑r、CH的長;
(2)如圖11,弦HQ交![]() 軸于點P,且DP:PH=3:2,求cos∠QHC的值;
軸于點P,且DP:PH=3:2,求cos∠QHC的值;
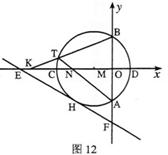
(3)如圖12,點K為線段EC上一動點(不與E、C重合),連接BK交⊙M于點T,弦AT交![]() 軸于點N。是否存在一個常數
軸于點N。是否存在一個常數![]() ,始終滿足MN·MK
,始終滿足MN·MK![]() ,如果存在,請求出
,如果存在,請求出![]() 的值;如果不存在,請說明理由。
的值;如果不存在,請說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com