
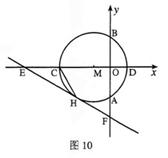
如圖10,以點M(-1,0)為圓心的圓與y軸、x軸分別交于點A、B、C、D,直線y=- x- 與⊙M相切于點H,交x軸于點E,交y軸于點F.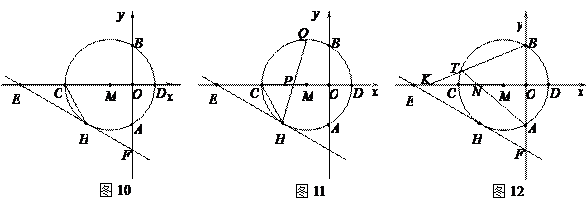
(1)請直接寫出OE、⊙M的半徑r、CH的長;(3分)
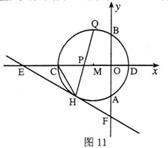
(2)如圖11,弦HQ交x軸于點P,且DP:PH=3:2,求cos∠QHC的值;(3分)
(3)如圖12,點K為線段EC上一動點(不與E、C重合),連接BK交⊙M于點T,弦AT交x軸于點N.是否存在一個常數a,始終滿足MN·MK=a,如果存在,請求出a的值;如果不存在,請說明理由.(3分)
 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖9,在平面直角坐標系中,二次函數的圖象的頂點為D點,與y軸交于C點,與x軸交于A、B兩點, A點在原點的左側,B點的坐標為(3,0),OB=OC ,tan∠ACO=
(1)求這個二次函數的表達式.
(2)經過C、D兩點的直線,與x軸交于點E,在該拋物線上是否存在這樣的點F,使以點A、C、E、F為頂點的四邊形為平行四邊形?若存在,請求出點F的坐標;若不存在,請說明理由.
(3)若平行于x軸的直線與該拋物線交于M、N兩點,且以MN為直徑的圓與x軸相切,求該圓半徑的長度.
(4)如圖10,若點G(2,y)是該拋物線上一點,點P是直線AG下方的拋物線上一動點,當點P運動到什么位置時,△APG的面積最大?求出此時P點的坐標和△APG的最大面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖10,以點M(—1,0)為圓心的圓與![]() 軸、
軸、![]() 軸分別交于點A、B、C、D,直線
軸分別交于點A、B、C、D,直線![]() 與⊙M相切于點H,交
與⊙M相切于點H,交![]() 軸于點E,求
軸于點E,求![]() 軸于點F。
軸于點F。
(1)請直接寫出OE、⊙M的半徑r、CH的長;
(2)如圖11,弦HQ交![]() 軸于點P,且DP:PH=3:2,求cos∠QHC的值;
軸于點P,且DP:PH=3:2,求cos∠QHC的值;
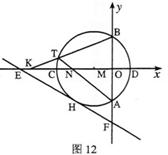
(3)如圖12,點K為線段EC上一動點(不與E、C重合),連接BK交⊙M于點T,弦AT交![]() 軸于點N。是否存在一個常數
軸于點N。是否存在一個常數![]() ,始終滿足MN·MK
,始終滿足MN·MK![]() ,如果存在,請求出
,如果存在,請求出![]() 的值;如果不存在,請說明理由。
的值;如果不存在,請說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com