
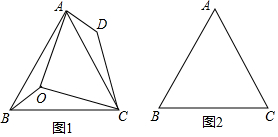
分析 (1)①根據旋轉變換的性質、四邊形內角和為360°計算即可;
②連接OD,根據勾股定理解答;
(2)①將△AOC繞點C按順時針方向旋轉60°得△A′O′C,連接OO′,根據等邊三角形的性質解答;
②根據等邊三角形的性質計算.
解答 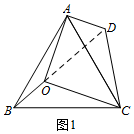 解:(1)①∵∠AOB=150°,∠BOC=120°,
解:(1)①∵∠AOB=150°,∠BOC=120°,
∴∠AOC=90°,
由旋轉的性質可知,∠OCD=60°,∠ADC=∠BOC=120°,
∴∠DAO=360°-60°-90°-120°=90°,
故答案為:90°;
②線段OA,OB,OC之間的數量關系是OA2+OB2=OC2.
如圖1,連接OD.
∵△BOC繞點C按順時針方向旋轉60°得△ADC,
∴△ADC≌△BOC,∠OCD=60°.
∴CD=OC,∠ADC=∠BOC=120°,AD=OB.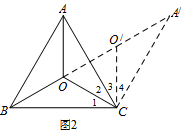
∴△OCD是等邊三角形,
∴OC=OD=CD,∠COD=∠CDO=60°,
∵∠AOB=150°,∠BOC=120°,
∴∠AOC=90°,
∴∠AOD=30°,∠ADO=60°.
∴∠DAO=90°.
在Rt△ADO中,∠DAO=90°,
∴OA2+AD2=OD2.
∴OA2+OB2=OC2.
(2)①如圖2,當α=β=120°時,OA+OB+OC有最小值.
作圖如圖2,
如圖2,將△AOC繞點C按順時針方向旋轉60°得△A′O′C,連接OO′.
∴△A′O′C≌△AOC,∠OCO′=∠ACA′=60°.
∴O′C=OC,O′A′=OA,A′C=BC,
∠A′O′C=∠AOC.
∴△OC O′是等邊三角形.
∴OC=O′C=OO′,∠COO′=∠CO′O=60°.
∵∠AOB=∠BOC=120°,
∴∠AOC=∠A′O′C=120°.
∴∠BOO′=∠OO′A′=180°.
∴四點B,O,O′,A′共線.
∴OA+OB+OC=O′A′+OB+OO′=BA′時值最小;
②當等邊△ABC的邊長為1時,OA+OB+OC的最小值A′B=$\sqrt{3}$.
點評 本題考查的是等邊三角形的性質、旋轉變換的性質,掌握等邊三角形的三個角是60°、三條邊相等是解題的關鍵.


 ABC考王全優卷系列答案
ABC考王全優卷系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
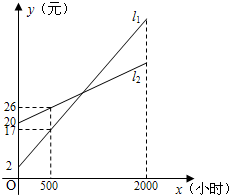 如圖所示,L1,L2分別表示一種白熾燈和一種節能燈的費用y(費用=燈的售價+電費,單位:元)與照明時間x(h)的函數關系圖象,假設兩種燈的使用壽命都是2000h,照明效果一樣.
如圖所示,L1,L2分別表示一種白熾燈和一種節能燈的費用y(費用=燈的售價+電費,單位:元)與照明時間x(h)的函數關系圖象,假設兩種燈的使用壽命都是2000h,照明效果一樣.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 元旦將至,某果品批發公司為指導今年的芒果銷售,對往年市場銷售情況進行了調查統計,得到如下數據:
元旦將至,某果品批發公司為指導今年的芒果銷售,對往年市場銷售情況進行了調查統計,得到如下數據:| 銷售價x(元/千克) | … | 25 | 24 | 23 | 22 | … |
| 銷售量y(千克) | … | 2000 | 2500 | 3000 | 3500 | … |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
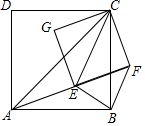 如圖,已知AC、EC分別為四邊形ABCD和EFCG的對角線,點E在△ABC內,∠CAE+∠CBE=90°,當四邊形ABCD和EFCG均為正方形時,連接BF.
如圖,已知AC、EC分別為四邊形ABCD和EFCG的對角線,點E在△ABC內,∠CAE+∠CBE=90°,當四邊形ABCD和EFCG均為正方形時,連接BF.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com