
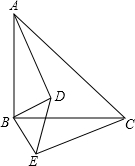
 如圖,△ABC和△DBE都是等腰三角形,BA=BC,BD=BE,且∠ABC=∠DBE.
如圖,△ABC和△DBE都是等腰三角形,BA=BC,BD=BE,且∠ABC=∠DBE.分析 (1)由條件證明△ABD≌△CBE,就可以得到結論;
(2)由△ABD≌△CBE就可以得出∠BAD=∠BCE,就可以得出∠FHC=90°,進而得出結論.
解答 (1)證明:∵∠ABC=∠DBE,
∴∠ABC-∠CBD=∠DBE-∠CBD,
∴∠ABD=∠CBE,
在△ABD和△CBE中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABD=∠CBE}\\{BD=BE}\end{array}\right.$,
∴△ABD≌△CBE(SAS),
∴AD=CE;
(2)AD⊥CE,理由是:
證明:延長AD交BC于F,交CE于H,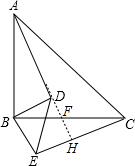
∵△ABD≌△ACE,
∴∠BAD=∠BCE.
∵∠CAB=90°,
∴∠BAD+∠AFB=90°,
∴∠BCE+∠AFB=90°.
∵∠CFH=∠AFB,
∴∠BCE+∠CFH=90°,
∴∠FHC=90°.
∴AD⊥CE;
點評 本題考查了全等三角形的判定及性質的運用,垂直的判定及性質的運用,等腰直角三角形的性質的運用,勾股定理的運用,解答時運用全等三角形的性質求解是關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
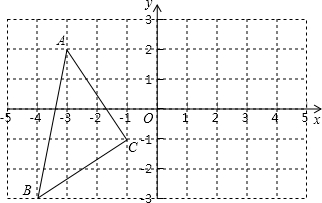 如圖,方格紙中的每個小方格都是邊長為1個單位長度的正方形,每個小正方形的頂點叫格點,△ABC的頂點均在格點上.
如圖,方格紙中的每個小方格都是邊長為1個單位長度的正方形,每個小正方形的頂點叫格點,△ABC的頂點均在格點上.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
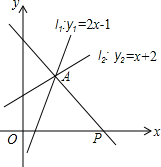 如圖,直線l1:y1=2x-1與直線l2:y2=x+2相交于點A,點P是x軸上任意一點,直線l3是經過點A和點P的一條直線.
如圖,直線l1:y1=2x-1與直線l2:y2=x+2相交于點A,點P是x軸上任意一點,直線l3是經過點A和點P的一條直線.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com