Question

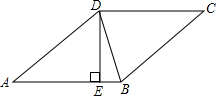
6．如圖所示，菱形ABCD的周長為20 cm，DE⊥AB，垂足為E，sinA=$\frac{3}{5}$，則下列結論錯誤的是（　　）

• A． DE=3 cm
• B． BE=1 cm
• C． 菱形的面積為15 cm²
• D． BD=2$\sqrt{10}{cm}$

Answer 1

分析 由菱形ABCD的周長為20 cm，推出AD=AB=5，由DE⊥AB，推出∠AED=90°，在Rt△ADE中，sin∠A=$\frac{3}{5}$=$\frac{DE}{AD}$，推出DE=3，AE=$\sqrt{A{D}^{2}-D{E}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4，推出EB=AB-AE=1，推出BD=$\sqrt{D{E}^{2}+E{B}^{2}}$=$\sqrt{10}$，推出菱形ABCD的面積=AB•DE=15．由此即可判斷．

解答 解：∵菱形ABCD的周長為20 cm，
∴AD=AB=5，
∵DE⊥AB，
∴∠AED=90°，
在Rt△ADE中，sin∠A=$\frac{3}{5}$=$\frac{DE}{AD}$，
∴DE=3，AE=$\sqrt{A{D}^{2}-D{E}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4，
∴EB=AB-AE=1，
∴BD=$\sqrt{D{E}^{2}+E{B}^{2}}$=$\sqrt{10}$，
∴菱形ABCD的面積=AB•DE=15．
故選D．

點評 本題考查菱形的判定、解直角三角形、勾股定理銳角三角函數等知識，解題的關鍵是靈活運用所學知識，屬于基礎題，中考常考題型．