
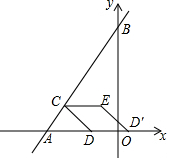
 如圖,在平面直角坐標系中,點A的坐標是(-3,0),點B的坐標是(0,4),動點C從點A出發沿射線AB方向以每秒1個單位的速度運動,過點C作CD⊥AB,交x軸于點D,點D關于y軸的對稱點為D′,以DC,DD′為邊作?CDD′E,設點C運動時間為t秒(t>0).
如圖,在平面直角坐標系中,點A的坐標是(-3,0),點B的坐標是(0,4),動點C從點A出發沿射線AB方向以每秒1個單位的速度運動,過點C作CD⊥AB,交x軸于點D,點D關于y軸的對稱點為D′,以DC,DD′為邊作?CDD′E,設點C運動時間為t秒(t>0).分析 (1)由△ACD∽△AOB,得$\frac{AC}{AO}$=$\frac{AD}{AB}$=$\frac{CD}{OB}$,$\frac{t}{3}$=$\frac{AD}{5}$=$\frac{CD}{4}$,求出AD、CD、OD,根據DD′=2OD即可解決問題.
(2)分兩種情形①如圖2中,當⊙P與DE相切時,②如圖3中,當⊙P與DE′相切時.分別構建方程即可解決問題.
(3)①如圖4中,當重疊部分是△CDF時,連接DE.當CF=EF時,S△CDF=$\frac{1}{4}$S四邊形CDD′E,求出t的值,②當t=$\frac{9}{5}$時,四邊形不存在.③如圖5中,當重疊部分是△ABD時,且S△ABD=$\frac{1}{4}$S四邊形CDD′E,求出t的值,由此即可解決問題.
解答 解:(1)如圖1中,當點D在線段OA上時.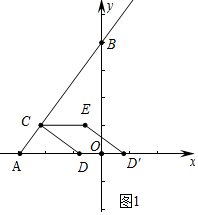
在Rt△ABC中,∵OA=3,OB=4,
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵∠A=∠A,∠ACD=∠AOB=90°,
∴△ACD∽△AOB,
∴$\frac{AC}{AO}$=$\frac{AD}{AB}$=$\frac{CD}{OB}$
∴$\frac{t}{3}$=$\frac{AD}{5}$=$\frac{CD}{4}$,
∴AD=$\frac{5}{3}$t,CD=$\frac{4}{3}$t,
∴OD=3-$\frac{5}{3}$t,
∵OD=OD′,
∴DD′=2OD=6-$\frac{10}{3}$t.
(2)①如圖2中,當⊙P與DE相切時,
∵∠EDD′=∠ACD=90°,∠ADC=∠ED′D,
∴△ACD∽△EDD′,
∴$\frac{AD}{ED′}$=$\frac{CD}{DD′}$,
∴$\frac{\frac{5}{3}t}{\frac{4}{3}t}$=$\frac{\frac{4}{3}t}{6-\frac{10}{3}t}$,
∴t=$\frac{15}{11}$.
②如圖3中,當⊙P與DE′相切時.
∵PE⊥D′E,CD∥ED′,
∴PE⊥CD,∵CD⊥AB,
∴AC∥PE,∵CE∥AP,
∴四邊形ACEP是平行四邊形,
∴AP=CE=DD′,
∴$\frac{1}{2}$•$\frac{5}{3}$t=6-$\frac{10}{3}$t,
∴t=$\frac{36}{25}$,
綜上所述,t=$\frac{15}{11}$s或$\frac{36}{25}$s時,⊙P與△DD′E的邊所在的直線相切.
(3)①如圖4中,當重疊部分是△CDF時,連接DE.
∵四邊形CDD′E是平行四邊形,
∴S△CED=S△DED′,
∴當CF=EF時,S△CDF=$\frac{1}{4}$S四邊形CDD′E,
∵CF∥AD,
∴$\frac{CF}{AD}$=$\frac{BC}{BA}$,
∴$\frac{\frac{1}{2}(6-\frac{10}{3}t)}{\frac{5}{3}t}$=$\frac{5-t}{5}$,
解得t=1或9(舍棄),
∴t=1.
②當t=$\frac{9}{5}$時,四邊形不存在.
③如圖5中,當重疊部分是△ABD時,且S△ABD=$\frac{1}{4}$S四邊形CDD′E,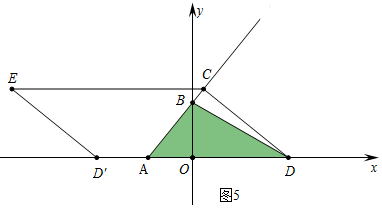
則有$\frac{1}{2}$•$\frac{5}{3}$t•4=$\frac{1}{4}$•($\frac{10}{3}$t-6)•$\frac{4}{5}$t,
解得t=$\frac{34}{5}$.
綜上所述,當1<t<$\frac{9}{5}$或$\frac{9}{5}$<t<$\frac{34}{5}$時,$\frac{{S}_{1}}{{S}_{2}}$>$\frac{1}{4}$.
點評 本題考查圓綜合題、切線的判定、平行四邊形的性質、相似三角形的判定和性質.三角形的面積等知識,解題的關鍵是學會用分類討論的思想思考問題,學會構建方程解決問題,屬于中考壓軸題.


科目:初中數學 來源: 題型:解答題
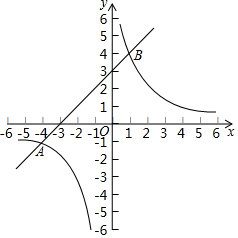 已知:如圖,在平面直角坐標系xOy中,反比例函數y1=$\frac{m}{x}$的圖象與一次函數y2=kx+b的圖象交于點A(-4,-1)和點B(1,n).
已知:如圖,在平面直角坐標系xOy中,反比例函數y1=$\frac{m}{x}$的圖象與一次函數y2=kx+b的圖象交于點A(-4,-1)和點B(1,n).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
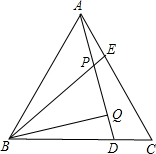 如圖,已知△ABC是等邊三角形,且AE=CD,AD、BE相交于P,BQ⊥AD于Q.
如圖,已知△ABC是等邊三角形,且AE=CD,AD、BE相交于P,BQ⊥AD于Q.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 小明和小亮用如圖所示的兩個轉盤(每個轉盤被分成三個面積相等的扇形)做游戲,轉動兩個轉盤各一次,若兩次數字之和為奇數,則小明勝;若兩次數字之和為偶數,則小亮勝,這個游戲對雙方公平嗎?說說你的理由.
小明和小亮用如圖所示的兩個轉盤(每個轉盤被分成三個面積相等的扇形)做游戲,轉動兩個轉盤各一次,若兩次數字之和為奇數,則小明勝;若兩次數字之和為偶數,則小亮勝,這個游戲對雙方公平嗎?說說你的理由.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知點A,C在反比例函數y=$\frac{a}{x}$(a>0)的圖象上,點B,D在反比例函數y=$\frac{b}{x}$(b<0)的圖象上,AB∥CD∥x軸,AB,CD在x軸的兩側,AB=3,CD=2,AB與CD的距離為5,則a-b的值是多少?
如圖,已知點A,C在反比例函數y=$\frac{a}{x}$(a>0)的圖象上,點B,D在反比例函數y=$\frac{b}{x}$(b<0)的圖象上,AB∥CD∥x軸,AB,CD在x軸的兩側,AB=3,CD=2,AB與CD的距離為5,則a-b的值是多少?查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com