Question

7．如圖，在平面直角坐標(biāo)系中，四邊形OADC是矩形，OA=6，AB=4，直線y=-x+3與坐標(biāo)軸交于D，E．設(shè)M是AB的中點(diǎn)，P是線段DE上的動(dòng)點(diǎn)，
（1）求M、D兩點(diǎn)的坐標(biāo)；
（2）當(dāng)P在什么位置時(shí)，PA=PB求出此時(shí)P點(diǎn)的坐標(biāo)；
（3）過P作PH⊥BC，垂足為H，當(dāng)以PM為直徑的⊙F與BC相切于點(diǎn)N時(shí)，求梯形PMBH的面積．

Answer 1

分析 （1）因?yàn)樗倪呅蜲ABC是矩形，OA=6，AB=4，直線3與坐標(biāo)軸交于D、E，M是AB的中點(diǎn)，求出M的坐標(biāo)；令y=0，即可求出D的坐標(biāo)；
（2）由題意得出P是AB的垂直平分線和直線ED的交點(diǎn)，而AB的中垂線是y=2，得P的縱坐標(biāo)為2，令直線ED的解析式中的y=2，求出的x的值即可；
（3）可設(shè)P（x，y），連接PN、MN、NF，因?yàn)辄c(diǎn)P在y=-x+3上，所以P（x，-x+3），根據(jù)題意可得PN⊥MN，F(xiàn)N⊥BC，F(xiàn)是圓心，又因N是線段HB的中點(diǎn)，HN=NB=$\frac{6-x}{2}$，PH=4-（-x+3）=x+1，BM=2，利用直徑對(duì)的圓周角是直角可得到∠HPN+∠HNP=∠HNP+∠BNM=90°，得出∠HPN=∠BNM，證出△PNH∽△NMB，得出對(duì)應(yīng)邊成比例，得到關(guān)于x的方程，解之即可求出x的值，即可求出梯形的面積．

解答 解：（1）∵四邊形OABC是矩形，OA=6，AB=4，M是AB的中點(diǎn)，
∴OA=6，AM=BM=2，
∴M（6，2）；
∵直線y=-x+3與坐標(biāo)軸交于D，E，
∴當(dāng)y=0時(shí)，-x+3=0，
解得：x=3，
∴D（3，0）；

（2）∵PA=PB，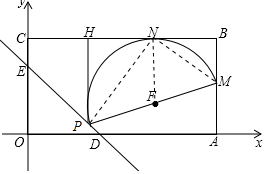
∴點(diǎn)P在線段AB的中垂線上，
∴點(diǎn)P的縱坐標(biāo)是2，
又∵點(diǎn)P在y=-x+3上，
∴2=-x+3，
∴x=1，
∴點(diǎn)P的坐標(biāo)為（ 1，2）；

（3）設(shè)P（x，y），連接PN、MN、NF，如圖所示：
∵點(diǎn)P在y=-x+3上，
∴P（x，-x+3），
依題意知：PN⊥MN，F(xiàn)N⊥BC，F(xiàn)是圓心，
∴N是線段HB的中點(diǎn)，HN=NB=$\frac{6-x}{2}$，PH=4-（-x+3）=x+1，BM=2，
∵∠HPN+∠HNP=∠HNP+∠BNM=90°，
∴∠HPN=∠BNM，
又∵∠PHN=∠B=90°，
∴Rt△PNH∽R(shí)t△NMB，
∴$\frac{HN}{BM}=\frac{PH}{BN}$，
∴$\frac{\frac{6-x}{2}}{2}=\frac{x+1}{\frac{6-x}{2}}$，
整理得：x²-20x+28=0，
解得：x=10+6$\sqrt{2}$（不合題意，舍去），或x=10-6$\sqrt{2}$，
∴梯形PMBH的面積=$\frac{1}{2}$（BM+PH）•BH=$\frac{1}{2}$（2+10-6$\sqrt{2}$+1）（6-10+6$\sqrt{2}$）=51$\sqrt{2}$-62．

點(diǎn)評(píng) 本題是圓的綜合題目題目，考查了矩形的性質(zhì)、坐標(biāo)與圖形性質(zhì)、一次函數(shù)的應(yīng)用、相似三角形的判定與性質(zhì)、一元二次方程的解法以及梯形面積的計(jì)算方法等知識(shí)；本題綜合性強(qiáng)，有一定難度．