某籃球隊12名隊員的年齡如表：
| 年齡（歲） | 18 | 19 | 20 | 21 |
| 人數 | 5 | 4 | 1 | 2 |
則這12名隊員年齡的眾數和平均數分別是（ ）
|
| A． | 18，19 | B． | 19，19 | C． | 18，19.5 | D． | 19，19.5 |
桃李文化快樂暑假武漢出版社系列答案科目：初中數學 來源： 題型：
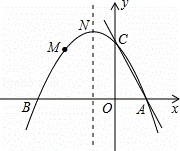
如圖，拋物線y=ax2+bx+c（a≠0）的圖象過點M（﹣2，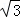
），頂點坐標為N（﹣1，
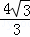），且與x軸交于A、B兩點，與y軸交于C點．
（1）求拋物線的解析式；
（2）點P為拋物線對稱軸上的動點，當△PBC為等腰三角形時，求點P的坐標；
（3）在直線AC上是否存在一點Q，使△QBM的周長最小？若存在，求出Q點坐標；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
如圖1，在平面直角坐標系中，二次函數y=﹣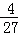
x2+12的圖象與y軸交于點A，與x軸交于B，C兩點（點B在點C的左側），連接AB，AC．
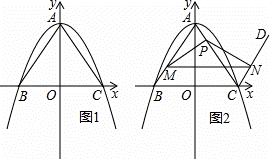
（1）點B的坐標為 ，點C的坐標為 ；
（2）過點C作射線CD∥AB，點M是線段AB上的動點，點P是線段AC上的動點，且始終滿足BM=AP（點M不與點A，點B重合），過點M作MN∥BC分別交AC于點Q，交射線CD于點N （點 Q不與點P重合），連接PM，PN，設線段AP的長為n．
①如圖2，當n＜
AC時，求證：△PAM≌△NCP；
②直接用含n的代數式表示線段PQ的長；
③若PM的長為
，當二次函數y=﹣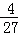x2+12的圖象經過平移同時過點P和點N時，請直接寫出此時的二次函數表達式．
查看答案和解析>>
科目：初中數學 來源： 題型：
某小區為了排污，需鋪設一段全長為720米的排污管道，為減少施工對居民生活的影響，須縮短施工時間，實際施工時每天的工作效率比原計劃提高20%，結果提前2天完成任務．設原計劃每天鋪設x米，下面所列方程正確的是（ ）
|
| A． |
| B． |
|
|
| C． |
| D． |
|
查看答案和解析>>
科目：初中數學 來源： 題型：
數學問題：計算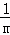
+
+
+…+
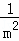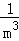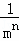（其中m，n都是正整數，且m≥2，n≥1）．
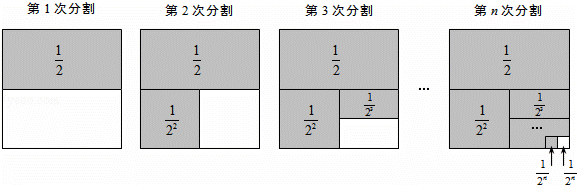
探究問題：為解決上面的數學問題，我們運用數形結合的思想方法，通過不斷地分割一個面積為1的正方形，把數量關系和幾何圖形巧妙地結合起來，并采取一般問題特殊化的策略來進行探究．
探究一：計算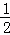
+
+
+…+
．
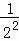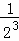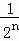第1次分割，把正方形的面積二等分，其中陰影部分的面積為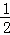
；
第2次分割，把上次分割圖中空白部分的面積繼續二等分，陰影部分的面積之和為+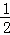
；
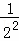第3次分割，把上次分割圖中空白部分的面積繼續二等分，…；
…
第n次分割，把上次分割圖中空白部分的面積最后二等分，所有陰影部分的面積之和為++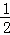
+…+
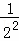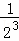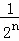，最后空白部分的面積是．
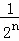根據第n次分割圖可得等式：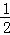
+
+
+…+
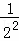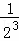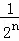=1﹣．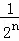
探究二：計算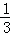
+
+
+…+
．
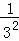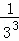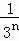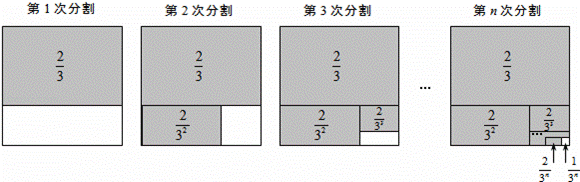
第1次分割，把正方形的面積三等分，其中陰影部分的面積為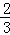
；
第2次分割，把上次分割圖中空白部分的面積繼續三等分，陰影部分的面積之和為+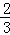
；
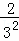第3次分割，把上次分割圖中空白部分的面積繼續三等分，…；
…
第n次分割，把上次分割圖中空白部分的面積最后三等分，所有陰影部分的面積之和為++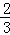
+…+
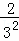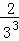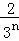，最后空白部分的面積是
．
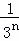根據第n次分割圖可得等式：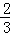
+
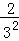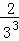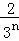++…+=1﹣，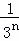
兩邊同除以2，得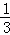
+
+
+…+
=
﹣
．
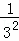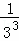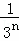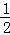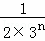探究三：計算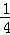
+
+
+…+
．
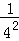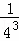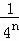（仿照上述方法，只畫出第n次分割圖，在圖上標注陰影部分面積，并寫出探究過程）
解決問題：計算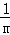
+
+
+…+
．
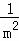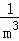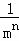（只需畫出第n次分割圖，在圖上標注陰影部分面積，并完成以下填空）
根據第n次分割圖可得等式：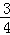 
+
+
+…+
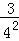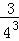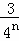=1﹣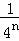
，
所以，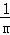
+
+
+…+
= 
﹣
．
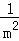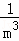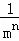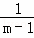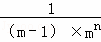拓廣應用：計算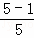 
+
+
+…+
．
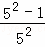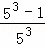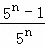查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
中，自變量x的取值范圍是 ．
﹣
=2
﹣
=