
數學問題:計算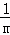 +
+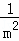 +
+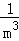 +…+
+…+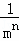 (其中m,n都是正整數,且m≥2,n≥1).
(其中m,n都是正整數,且m≥2,n≥1).
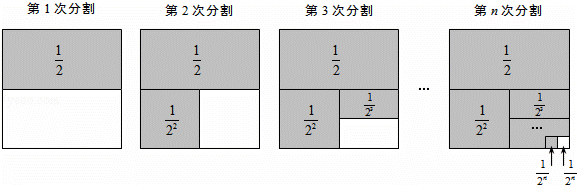
探究問題:為解決上面的數學問題,我們運用數形結合的思想方法,通過不斷地分割一個面積為1的正方形,把數量關系和幾何圖形巧妙地結合起來,并采取一般問題特殊化的策略來進行探究.
探究一:計算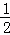 +
+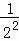 +
+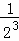 +…+
+…+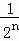 .
.
第1次分割,把正方形的面積二等分,其中陰影部分的面積為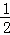 ;
;
第2次分割,把上次分割圖中空白部分的面積繼續二等分,陰影部分的面積之和為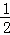 +
+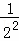 ;
;
第3次分割,把上次分割圖中空白部分的面積繼續二等分,…;
…
第n次分割,把上次分割圖中空白部分的面積最后二等分,所有陰影部分的面積之和為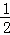 +
+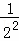 +
+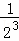 +…+
+…+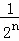 ,最后空白部分的面積是
,最后空白部分的面積是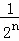 .
.
根據第n次分割圖可得等式: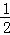 +
+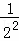 +
+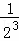 +…+
+…+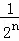 =1﹣
=1﹣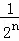 .
.
探究二:計算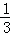 +
+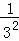 +
+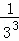 +…+
+…+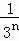 .
.
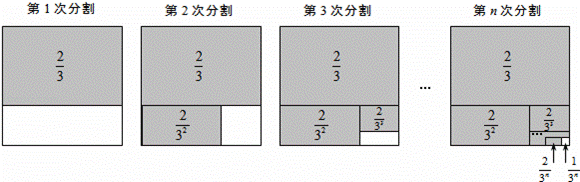
第1次分割,把正方形的面積三等分,其中陰影部分的面積為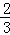 ;
;
第2次分割,把上次分割圖中空白部分的面積繼續三等分,陰影部分的面積之和為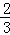 +
+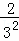 ;
;
第3次分割,把上次分割圖中空白部分的面積繼續三等分,…;
…
第n次分割,把上次分割圖中空白部分的面積最后三等分,所有陰影部分的面積之和為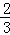 +
+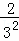 +
+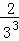 +…+
+…+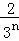 ,最后空白部分的面積是
,最后空白部分的面積是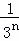 .
.
根據第n次分割圖可得等式: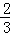 +
+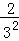 +
+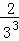 +…+
+…+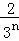 =1﹣
=1﹣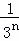 ,
,
兩邊同除以2,得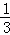 +
+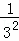 +
+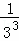 +…+
+…+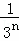 =
=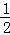 ﹣
﹣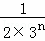 .
.
探究三:計算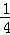 +
+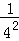 +
+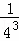 +…+
+…+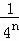 .
.
(仿照上述方法,只畫出第n次分割圖,在圖上標注陰影部分面積,并寫出探究過程)

解決問題:計算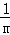 +
+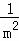 +
+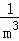 +…+
+…+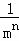 .
.
(只需畫出第n次分割圖,在圖上標注陰影部分面積,并完成以下填空)
根據第n次分割圖可得等式: 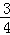 +
+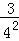 +
+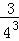 +…+
+…+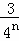 =1﹣
=1﹣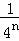 ,
,
所以,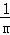 +
+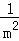 +
+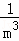 +…+
+…+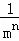 =
= 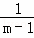 ﹣
﹣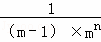 .
.
拓廣應用:計算 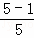 +
+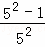 +
+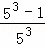 +…+
+…+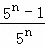 .
.
解:探究三:第1次分割,把正方形的面積四等分,

其中陰影部分的面積為 ;
;
第2次分割,把上次分割圖中空白部分的面積繼續四等分,
陰影部分的面積之和為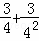 ;
;
第3次分割,把上次分割圖中空白部分的面積繼續四等分,
…,
第n次分割,把上次分割圖中空白部分的面積最后四等分,
所有陰影部分的面積之和為: +
+ +
+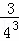 +…+
+…+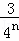 ,
,
最后的空白部分的面積是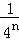 ,
,
根據第n次分割圖可得等式: +
+ +
+ +…+
+…+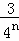 =1﹣
=1﹣ ,
,
兩邊同除以3,得 +
+ +
+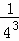 +…+
+…+ =
=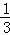 ﹣
﹣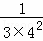 ;
;
解決問題: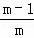 +
+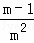 +
+ +…+
+…+ =1﹣
=1﹣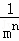 ,
,
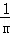 +
+ +
+ +…+
+…+ =
=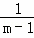 ﹣
﹣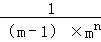 ;
;
故答案為: +
+ +
+ +…+
+…+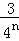 =1﹣
=1﹣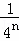 ,
,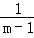 ﹣
﹣ ;
;

拓廣應用: +
+ +
+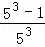 +…+
+…+ ,
,
=1﹣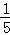 +1﹣
+1﹣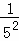 +1﹣
+1﹣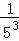 +…+1﹣
+…+1﹣ ,
,
=n﹣(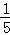 +
+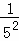 +
+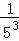 +…+
+…+ ),
),
=n﹣( ﹣
﹣ ),
),
=n﹣ +
+ .
.


 桃李文化快樂暑假武漢出版社系列答案
桃李文化快樂暑假武漢出版社系列答案 優秀生快樂假期每一天全新寒假作業本系列答案
優秀生快樂假期每一天全新寒假作業本系列答案 暑假接力賽新疆青少年出版社系列答案
暑假接力賽新疆青少年出版社系列答案科目:初中數學 來源: 題型:
某籃球隊12名隊員的年齡如表:
| 年齡(歲) | 18 | 19 | 20 | 21 |
| 人數 | 5 | 4 | 1 | 2 |
則這12名隊員年齡的眾數和平均數分別是( )
|
| A. | 18,19 | B. | 19,19 | C. | 18,19.5 | D. | 19,19.5 |
查看答案和解析>>
科目:初中數學 來源: 題型:
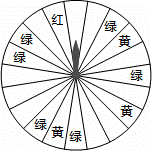
某商場為了吸引顧客,設立了可以自由轉動的轉盤(如圖,轉盤被均勻分為20份),并規定:顧客每購買200元的商品,就能獲得一次轉動轉盤的機會.如果轉盤停止后,指針正好對準紅色、黃色、綠色區域,那么顧客就可以分別獲得200元、100元、50元的購物券,憑購物券可以在該商場繼續購物.如果顧客不愿意轉轉盤,那么可以直接獲得購物券30元.
(1)求轉動一次轉盤獲得購物券的概率;
(2)轉轉盤和直接獲得購物券,你認為哪種方式對顧客更合算?
查看答案和解析>>
科目:初中數學 來源: 題型:
矩形紙片ABCD中,已知AD=8,AB=6,E是邊BC上的點,以AE為折痕折疊紙片,使點B落在點F處,連接FC,當△EFC為直角三角形時,BE的長為
查看答案和解析>>
科目:初中數學 來源: 題型:
據統計我國2014年前四月已開工建造286萬套保障房,其中286萬用科學記數法表示為( )
|
| A. | 2.86×106 | B. | 2.86×107 | C. | 28.6×105 | D. | 0.286×107 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com