
 如圖,在平行四邊形ABCD中,AB=5,AD=2,∠B=60°,以點B為圓心,BC為半徑的圓弧交AB于點E,連接DE,則圖中陰影部分的面積為$\frac{7}{2}$$\sqrt{3}$-$\frac{3}{2}$π.(結果保留π)
如圖,在平行四邊形ABCD中,AB=5,AD=2,∠B=60°,以點B為圓心,BC為半徑的圓弧交AB于點E,連接DE,則圖中陰影部分的面積為$\frac{7}{2}$$\sqrt{3}$-$\frac{3}{2}$π.(結果保留π) 分析 過點C作CF⊥BA,易求平行四邊形ABCD、扇形CBE、△DAE的面積,利用陰影部分的面積=平行四邊形的面積-扇形面積-△DAE面積計算即可.
解答 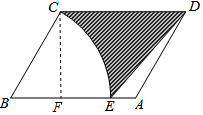 解:過點A作AF⊥BC,
解:過點A作AF⊥BC,
∵BC=AD=2,∠B=60°,
∴CF=$\sqrt{3}$,
∴平行四邊形ABCD面積=AB•CF=5$\sqrt{3}$,
∴扇形ABE面積=$\frac{60π×{2}^{2}}{360}$=$\frac{2}{3}$π,
∵AD=BC=2,BE=2,
∴AE=3,
∴△DAE的面積=$\frac{1}{2}$AE•CF=$\frac{3}{2}$$\sqrt{3}$,
∴陰影部分的面積=平行四邊形的面積-扇形面積-△DAE面積=5$\sqrt{3}$-$\frac{2}{3}$π-$\frac{3}{2}$$\sqrt{3}$=$\frac{7}{2}$$\sqrt{3}$-$\frac{3}{2}$π,
故答案為:$\frac{7}{2}$$\sqrt{3}$-$\frac{3}{2}$π.
點評 本題考查了平行四邊形的性質、扇形的面積公式運用、三角形面積公式運用,解題的關鍵是作平行四邊形的高線,構造直角三角形,并且求出其高線的長度.


 桃李文化快樂暑假武漢出版社系列答案
桃李文化快樂暑假武漢出版社系列答案 優秀生快樂假期每一天全新寒假作業本系列答案
優秀生快樂假期每一天全新寒假作業本系列答案 暑假接力賽新疆青少年出版社系列答案
暑假接力賽新疆青少年出版社系列答案科目:初中數學 來源: 題型:選擇題
| A. | $\frac{9}{2}$$\sqrt{2}$ | B. | -$\frac{7}{2}$$\sqrt{2}$ | C. | $\frac{9}{\sqrt{2}}$ | D. | -$\frac{7}{\sqrt{2}}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
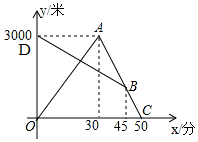 某天早晨,張強從家跑步去體育鍛煉,同時媽媽從體育場晨練結束回家,途中兩人相遇,張強跑到體育場后發現要下雨,立即按原路返回,遇到媽媽后兩人一起回到家(張強和媽媽始終在同一條筆直的公路上行走).如圖是兩人離家的距離y(米)與張強出發的時間x(分)之間的函數圖象,根據圖象信息解答下列問題:
某天早晨,張強從家跑步去體育鍛煉,同時媽媽從體育場晨練結束回家,途中兩人相遇,張強跑到體育場后發現要下雨,立即按原路返回,遇到媽媽后兩人一起回到家(張強和媽媽始終在同一條筆直的公路上行走).如圖是兩人離家的距離y(米)與張強出發的時間x(分)之間的函數圖象,根據圖象信息解答下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
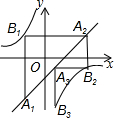 如圖,已知:n為正整數,點A1(x1,y1),A2(x2,y2),A3(x3,y3),A4(x4,y4)…An(xn,yn)均在直線y=x-1上,點B1(m1,p1),B2(m2,p2),B3(m3,p3)…Bn(mn,pn)均在雙曲線y=-$\frac{1}{x}$上,并且滿足:A1B1⊥x軸,B1A2⊥y軸,A2B2⊥x軸,B2A3⊥y軸,A3B3⊥x軸,…,AnBn⊥x軸,BnAn+1⊥y軸,若點A1的橫坐標為-1,則點A2017的坐標為( )
如圖,已知:n為正整數,點A1(x1,y1),A2(x2,y2),A3(x3,y3),A4(x4,y4)…An(xn,yn)均在直線y=x-1上,點B1(m1,p1),B2(m2,p2),B3(m3,p3)…Bn(mn,pn)均在雙曲線y=-$\frac{1}{x}$上,并且滿足:A1B1⊥x軸,B1A2⊥y軸,A2B2⊥x軸,B2A3⊥y軸,A3B3⊥x軸,…,AnBn⊥x軸,BnAn+1⊥y軸,若點A1的橫坐標為-1,則點A2017的坐標為( )| A. | (-1,-2) | B. | (2,1) | C. | ($\frac{1}{2}$,$-\frac{1}{2}$) | D. | ($\frac{1}{2}$,-2) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com