
注意:為了使同學們更好地解答本題,我們提供了一種解題思路,你可以依照這個思路按下面的要求填空,完成本題的解答.也可以選用其他的解題方案,此時不必填空,只需按照解答題的一般要求進行解答.
要組織一次排球邀請賽,參賽的每兩個隊之間都要比賽一場.根據場地和時間等條件,賽程計劃安排7天,每天安排4場比賽,比賽組織者應邀多少個隊參賽?
解題方案:
設比賽組織者應邀請x個隊參賽,
(1)用含x的代數式表示:
那么每個隊要與其他 個隊各賽一場,又由于甲隊對乙隊的比賽和乙隊對甲對的比賽是同一場比賽,所以全部的比賽一共有 場;
(2)根據題意,列出相應方程;
(3)解這個方程,得;
(4)檢驗: ;
(5)答: .
【考點】一元二次方程的應用.
【分析】可設比賽組織者應邀請x隊參賽,則每個隊參加(x﹣1)場比賽,則共有
 x(x﹣1)場比賽,可以列出一個一元二次方程,求解,舍去小于0的值,即可得所求的結果.
x(x﹣1)場比賽,可以列出一個一元二次方程,求解,舍去小于0的值,即可得所求的結果.
【解答】解:設比賽組織者應邀請x個隊參賽,
(1)用含x的代數式表示:
那么每個隊要與其他(x﹣1)個隊各賽一場,又由于甲隊對乙隊的比賽和乙隊對甲對的比賽是同一場比賽,所以全部的比賽一共有28場;
(2)根據題意,列出相應方程:
 x(x﹣1)=28,
x(x﹣1)=28,
(3)解這個方程,得:x1=8,x2=﹣7,
(4)檢驗:x2=﹣7(舍去);
(5)答:比賽組織者應邀請8隊參賽.
故答案為:(x﹣1);28;
 x(x﹣1)=28;x1=8,x2=﹣7;x2=﹣7(舍去);比賽組織者應邀請8隊參賽.
x(x﹣1)=28;x1=8,x2=﹣7;x2=﹣7(舍去);比賽組織者應邀請8隊參賽.
【點評】此題主要考查了一元二次方程的應用,解決本題的關鍵是得到比賽總場數的等量關系,注意2隊之間的比賽只有1場,最后的總場數應除以2.


 尖子生新課堂課時作業系列答案
尖子生新課堂課時作業系列答案 英才計劃同步課時高效訓練系列答案
英才計劃同步課時高效訓練系列答案科目:初中數學 來源: 題型:
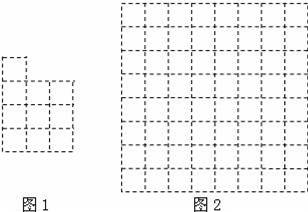
現有10個邊長為1的正方形,排列形式如圖1,請把它們分割后拼接成一個新的正方形.要求:在圖1中用實線畫出分割線,并在圖2的正方形網格圖(圖中每個小正方形的邊長均為1)中用實線畫出拼接成的新正方形.

查看答案和解析>>
科目:初中數學 來源: 題型:
已知A,B,C是⊙O上的三個點,四邊形OABC是平行四邊形,那么下列結論中錯誤的是( )
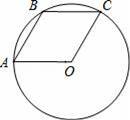

A.∠AOC=120°
B.四邊形OABC一定是菱形
C.若連接AC,則AC=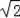
 OA
OA
D.若連接AC、BO,則AC與BO互相垂直平分
查看答案和解析>>
科目:初中數學 來源: 題型:
有五張下面分別標有數字﹣2,0,
 ,1,3的不透明卡片,它們除數字不同外其余全部相同.現將它們背面朝上,洗勻后從中任取一張,將該卡片上的數字記為a,則使關于x的分工方程
,1,3的不透明卡片,它們除數字不同外其余全部相同.現將它們背面朝上,洗勻后從中任取一張,將該卡片上的數字記為a,則使關于x的分工方程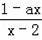
 +2=
+2=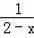
 有整數解的概率是 .
有整數解的概率是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,在五邊形ABCDE中,∠A+∠B+∠E=300°,DP、CP分別平分∠EDC、∠BCD,則∠P的度數是( )
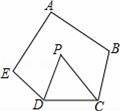

A.60° B.65° C.55° D.50°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com