
分析 (1)設S=1+3+5+…+(2n-1)①,則S=(2n-1)+(2n-3)+(2n-5)+…+1 ②,①+②得出2S=$\underset{\underbrace{2n+2n+2n+…+2n}}{n個}$=2n2,即可得證;
(2)設x=2n-1,則1+3+5+…+2n-1=n2=361,解之得出n的值,代入x=2n-1即可.
解答 解:(1)設S=1+3+5+…+(2n-1),①
則S=(2n-1)+(2n-3)+(2n-5)+…+1,②
①+②,得:2S=$\underset{\underbrace{2n+2n+2n+…+2n}}{n個}$=2n2,
∴S=n2,即1+3+5+…+(2n-1)=n2;
(2)設x=2n-1,
則1+3+5+…+2n-1=n2=361,
解得:n=19或n=-19(舍),
∴x=2n-1=38-1=37.
點評 本題主要考查數字的變化規律及整式的運算、解方程的能力,弄清題干中求和的方法、并熟練運用是解題的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
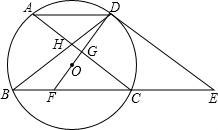 如圖,⊙O的弦AD∥BC,過點D的切線交BC的延長線于點E,AC∥DE交BD于點H,DO及延長線分別交AC、BC于點G、F.
如圖,⊙O的弦AD∥BC,過點D的切線交BC的延長線于點E,AC∥DE交BD于點H,DO及延長線分別交AC、BC于點G、F.查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
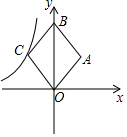 如圖,在平面直角坐標中,菱形OABC的面積為12,點B在y軸上,點C在反比例函數y=$\frac{k}{x}$的圖象上,則k的值為( )
如圖,在平面直角坐標中,菱形OABC的面積為12,點B在y軸上,點C在反比例函數y=$\frac{k}{x}$的圖象上,則k的值為( )| A. | 3 | B. | -3 | C. | 6 | D. | -6 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
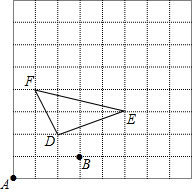 如圖,用(0,0)表示A點的位置,用(3,1)表示B點的位置,那么:
如圖,用(0,0)表示A點的位置,用(3,1)表示B點的位置,那么:查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
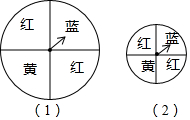 如圖,兩個用來搖獎的轉盤,其中說法正確的是( )
如圖,兩個用來搖獎的轉盤,其中說法正確的是( )| A. | 轉盤(1)中藍色區域的面積比轉盤(2)中的藍色區域面積要大,所以搖轉盤(1)比搖轉盤(2)時,藍色區域得獎的可能性大 | |
| B. | 兩個轉盤中指針指向藍色區域的機會一樣大 | |
| C. | 轉盤(1)中,指針指向紅色區域的概率是$\frac{1}{3}$ | |
| D. | 在轉盤(2)中只有紅、黃、藍三種顏色,指針指向每種顏色的概率都是$\frac{1}{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com