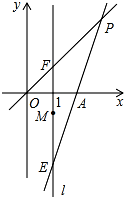Question

16．如圖，在平面直角坐標系中，O為原點，直線l：x=1，點A（2，0），點E，F，M都在直線l上，且點E和點F關于點M對稱．若點M坐標為（1，-1），直線EA與直線OF交于點P．
（1）當點F的坐標為（1，1）時，如圖，求點P的坐標；
（2）當點F為直線l上的動點時，記點P（x，y），求y關于x的函數解析式．

Answer 1

分析 （1）利用對稱的性質得到E（1，-3），再利用待定系數法求出直線EA的解析式為y=3x-6．直線OF的解析式為y=x，利用兩直線相交的問題，通過解方程組$\left\{\begin{array}{l}{y=x}\\{y=3x-6}\end{array}\right.$可得到點P的坐標；
（2）由已知可設點F的坐標是（1，t），與（1）一樣，利用對稱的性質得到E（1，-2-2t），再利用待定系數法求出直線EA的解析式為y=（2+t）x-4-2t，直線OF的解析式為y=tx，利用兩直線相交的問題得到tx=（2+t）x-2（2+t），即t=x-2，于是得到y=tx=（x-2）x=x²-2x．

解答 解：（1）∵點E和點F關于點M（1，-1）對稱，
而F（1，1），
∴E（1，-3），
設直線EA的解析式為：y=kx+b（k≠0）、
把E（1，-3），A（2，0）代入得$\left\{\begin{array}{l}{k+b=-3}\\{2k+b=0}\end{array}\right.$，解得$\left\{\begin{array}{l}{k=3}\\{b=-6}\end{array}\right.$，
∴直線EA的解析式為：y=3x-6．
∵點O（0，0），F（1，1），
∴直線OF的解析式為y=x，
解方程組$\left\{\begin{array}{l}{y=x}\\{y=3x-6}\end{array}\right.$得$\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$，
∴點P的坐標是（3，3）；
（2）由已知可設點F的坐標是（1，t）．
∴直線OF的解析式為y=tx，
由點E和點F關于點M（1，-1）對稱，得點E（1，-2-t）．
設直線EA的解析式為y=cx+d（c、d是常數，且c≠0），
把E（1，-2-t），A（2，0）代入得$\left\{\begin{array}{l}{c+d=-2-t}\\{2c+d=0}\end{array}\right.$，解得$\left\{\begin{array}{l}{c=2+t}\\{d=-4-2t}\end{array}\right.$，
∴直線EA的解析式為：y=（2+t）x-4-2t，
∵點P為直線OF與直線EA的交點，
∴tx=（2+t）x-2（2+t），即t=x-2．
∴y=tx=（x-2）x=x²-2x．

點評 本題考查了兩直線相交或平行問題：兩條直線的交點坐標，就是由這兩條直線相對應的一次函數表達式所組成的二元一次方程組的解；若兩條直線是平行的關系，那么他們的自變量系數相同，即k值相同．也考查了待定系數法求一次函數解析式．