
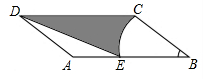
 如圖,在平行四邊形ABCD中,AB=5,AD=2,∠B=60°,以點B為圓心,BG為半徑的圓弧交AB于點E,連接DE,則圖中陰影部分的面積為$\frac{7\sqrt{3}}{2}$-$\frac{2}{3}$π.(結(jié)果保留π)
如圖,在平行四邊形ABCD中,AB=5,AD=2,∠B=60°,以點B為圓心,BG為半徑的圓弧交AB于點E,連接DE,則圖中陰影部分的面積為$\frac{7\sqrt{3}}{2}$-$\frac{2}{3}$π.(結(jié)果保留π) 分析 作CH⊥AB于H,根據(jù)正弦的概念求出CH,根據(jù)扇形面積公式、三角形的面積公式計算即可.
解答 解: 作CH⊥AB于H,
作CH⊥AB于H,
則CH=BC×sinB=$\sqrt{3}$,
由題意得,AE=AB-BE=3,
∴平行四邊形ABCD的面積AB×CH=5$\sqrt{3}$,
則陰影部分的面積為:5$\sqrt{3}$-$\frac{1}{2}$×AE×CH-$\frac{60π×{2}^{2}}{360}$=$\frac{7\sqrt{3}}{2}$-$\frac{2}{3}$π,
故答案為:$\frac{7\sqrt{3}}{2}$-$\frac{2}{3}$π.
點評 本題考查的是平行四邊形的性質(zhì)、扇形面積的計算,掌握扇形的面積公式S=$\frac{nπ{R}^{2}}{360}$是解題的關(guān)鍵.


 云南師大附小一線名師提優(yōu)作業(yè)系列答案
云南師大附小一線名師提優(yōu)作業(yè)系列答案 沖刺100分單元優(yōu)化練考卷系列答案
沖刺100分單元優(yōu)化練考卷系列答案科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| 分數(shù) | 75 | 80 | 85 | 90 |
| 人數(shù) | 1 | 4 | 3 | 2 |
| A. | 80 | B. | 82.5 | C. | 85 | D. | 87.5 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
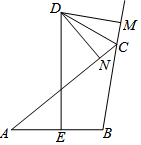 已知,如圖,DE為△ABC的邊AB的垂直平分線,CD為△ABC的外角平分線,與DE交于D,DM⊥BC于M,DN⊥AC于N,若CM=1,BC=3,求AN的長.
已知,如圖,DE為△ABC的邊AB的垂直平分線,CD為△ABC的外角平分線,與DE交于D,DM⊥BC于M,DN⊥AC于N,若CM=1,BC=3,求AN的長.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | ①② | B. | ①③ | C. | ①④ | D. | ②④ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 0.201×10-6cm | B. | 2.01×10-6cm | C. | 0.201×10-7cm | D. | 2.01×10-7cm |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com