
 如圖,△ABC中,∠ACB=90°,BC=4,AC=8,△FDE≌△ABC.△FDE頂點(diǎn)D與邊AB的中點(diǎn)重合,DE,DF分別交AC于點(diǎn)P,Q,若重疊部分△DPQ是以DP為一腰的等腰三角形,則它的面積為$\frac{5}{2}$或2$\sqrt{5}$-2.
如圖,△ABC中,∠ACB=90°,BC=4,AC=8,△FDE≌△ABC.△FDE頂點(diǎn)D與邊AB的中點(diǎn)重合,DE,DF分別交AC于點(diǎn)P,Q,若重疊部分△DPQ是以DP為一腰的等腰三角形,則它的面積為$\frac{5}{2}$或2$\sqrt{5}$-2. 分析 分兩種情況:
①當(dāng)PD=PQ時(shí),如圖1所示:
過點(diǎn)D作DK⊥AC于點(diǎn)K,則DK∥BC,作輔助線,利用相似三角形、勾股定理、等腰三角形的性質(zhì),列方程求解;
②當(dāng)PD=DQ時(shí),如圖2,用輔助線,利用等腰三角形三線合一的性質(zhì)和平行線的性質(zhì)得:∠FDM=∠EDM,∠NMD=∠EDM,設(shè)MN=DN=x,利用同角的三角函數(shù)表示FN=4$\sqrt{5}$-x,由勾股定理列方程求出x的值,從而求得S△PDQ的值.
解答 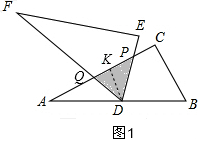 解:分兩種情況:
解:分兩種情況:
①當(dāng)PD=PQ時(shí),如圖1所示:
過點(diǎn)D作DK⊥AC于點(diǎn)K,則DK∥BC,
又∵點(diǎn)D為AB中點(diǎn),
∴DK=$\frac{1}{2}$BC=$\frac{1}{2}×4$=2,
∵PD=PQ,
∴∠PQD=∠PDQ,由∠PDQ=∠B,
∴∠PQD=∠B,
又∵∠DKQ=∠C=90°,
∴△DKQ∽△ACB,
∴$\frac{KQ}{BC}=\frac{DK}{AC}$,即$\frac{KQ}{4}=\frac{2}{8}$,得KQ=1,
設(shè)PD=PQ=x,則PK=x-1,
在Rt△DMK中,由勾股定理得:PK2+DK2=PD2,
即:(x-1)2+22=x2,解得x=$\frac{5}{2}$,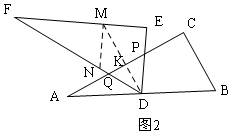
∴S△PDQ=$\frac{1}{2}$PQ•DK=$\frac{1}{2}$×$\frac{5}{2}$×2=$\frac{5}{2}$.
②當(dāng)PD=DQ時(shí),如圖2所示,
過D作DK⊥AC,交AC于K,交EF于M,過M作MN⊥EF,交DF于N,則MN∥DE,
∴∠FDM=∠EDM,∠NMD=∠EDM,
∴∠FDM=∠NMD,
∴MN=DN,
設(shè)MN=DN=x,
tan∠F=$\frac{DE}{EF}=\frac{MN}{FM}$=$\frac{4}{8}=\frac{1}{2}$,
∴FM=2x,
∵FD=AB=4$\sqrt{5}$,
∴FN=4$\sqrt{5}$-x,
在Rt△FMN中,由勾股定理得:FN2=FM2+MN2,
$(4\sqrt{5}-x)^{2}={x}^{2}+(2x)^{2}$,
解得:x=5-$\sqrt{5}$,
∴ME=EF-FM=8-2x=2$\sqrt{5}$-2,
由①得:DK=2,
tan∠MDE=$\frac{ME}{DE}=\frac{KP}{DK}$,
∴$\frac{2\sqrt{5}-2}{4}=\frac{KP}{2}$,
∴KP=$\sqrt{5}$-1,
∵PD=DQ,DK⊥PQ,
∴PQ=2KP=2$\sqrt{5}$-2,
∴S△PDQ=$\frac{1}{2}$PQ•DK=$\frac{1}{2}$(2$\sqrt{5}$-2)×2=2$\sqrt{5}$-2,
綜上所述,重疊部分△DPQ的面積是$\frac{5}{2}$或2$\sqrt{5}$-2;
故答案為:$\frac{5}{2}$或2$\sqrt{5}$-2.
點(diǎn)評 此題主要考查了旋轉(zhuǎn)的性質(zhì)以及相似三角形的性質(zhì)和勾股定理等知識,等腰三角形的定義采用分情況討論的方式,作輔助線,構(gòu)建直角三角形,利用勾股定理得出方程是解題關(guān)鍵.


 浙大優(yōu)學(xué)小學(xué)年級銜接導(dǎo)與練浙江大學(xué)出版社系列答案
浙大優(yōu)學(xué)小學(xué)年級銜接導(dǎo)與練浙江大學(xué)出版社系列答案 小學(xué)暑假作業(yè)東南大學(xué)出版社系列答案
小學(xué)暑假作業(yè)東南大學(xué)出版社系列答案 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案 波波熊暑假作業(yè)江西人民出版社系列答案
波波熊暑假作業(yè)江西人民出版社系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
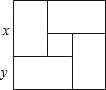 用四個(gè)全等的矩形和一個(gè)小正方形拼成如圖所示的大正方形.已知大正方形的面積是196,小正方形的面積是4,若用x,y表示矩形的長和寬(x>y),則下列關(guān)系式中不正確的是( )
用四個(gè)全等的矩形和一個(gè)小正方形拼成如圖所示的大正方形.已知大正方形的面積是196,小正方形的面積是4,若用x,y表示矩形的長和寬(x>y),則下列關(guān)系式中不正確的是( )| A. | x+y=14 | B. | x-y=2 | C. | xy=48 | D. | x2+y2=144 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 南邊,-1.5km | B. | 北邊、-1.5km | C. | 南邊、1.5km | D. | 北邊、1.5km |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
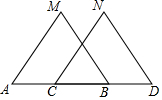 如圖,已知MB=ND,∠MBA=∠NDC,下列條件中不能判定△ABM≌△CDN的是( )
如圖,已知MB=ND,∠MBA=∠NDC,下列條件中不能判定△ABM≌△CDN的是( )| A. | ∠M=∠N | B. | AM∥CN | C. | AB=CD | D. | AM=CN |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com