Question

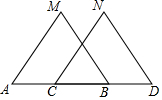
14．如圖，已知MB=ND，∠MBA=∠NDC，下列條件中不能判定△ABM≌△CDN的是（　　）

• A． ∠M=∠N
• B． AM∥CN
• C． AB=CD
• D． AM=CN

Answer 1

分析 根據三角形全等的判定定理，有AAS、SSS、ASA、SAS四種．逐條驗證即可．

解答 解：A、∠M=∠N，符合ASA，能判定△ABM≌△CDN，故A選項不符合題意；
B、AM∥CN，得出∠MAB=∠NCD，符合AAS，能判定△ABM≌△CDN，故D選項不符合題意．
C、AB=CD，符合SAS，能判定△ABM≌△CDN，故B選項不符合題意；
D、根據條件AM=CN，MB=ND，∠MBA=∠NDC，不能判定△ABM≌△CDN，故C選項符合題意；
故選D．

點評 本題重點考查了三角形全等的判定定理，普通兩個三角形全等共有四個定理，即AAS、ASA、SAS、SSS，直角三角形可用HL定理，本題是一道較為簡單的題目．