
分析 (1)①設購進A種計算器x臺,則購進B種計算器(50-x)臺,根據總錢數=購進A種計算機的錢數+購進B種計算機的錢數即可列出關于x的一元一次方程,解之即可得出結論;
②設購進A種計算器y臺,則購進C種計算器(50-y)臺,根據總錢數=購進A種計算機的錢數+購進C種計算機的錢數即可列出關于y的一元一次方程,解之即可得出結論;
(2)當只購進B、C兩種型號時,設購進B種計算器z臺,則購進C種計算器(50-z)臺,根據總錢數=購進B種計算機的錢數+購進C種計算機的錢數即可列出關于z的一元一次方程,解之即可得出z的值,從而得出此種進貨方式不合理;當只購進A、B兩種型號時,根據總利潤=銷售A種計算器的利潤+銷售B種計算器的利潤即可算出選此方案時的利潤;當只購進A、C兩種型號時,根據總利潤=銷售A種計算器的利潤+銷售C種計算器的利潤即可算出選此方案時的利潤.二者比較后即可得出結論.
解答 (1)①設購進A種計算器x臺,則購進B種計算器(50-x)臺,
根據題意得:15x+21(50-x)=900,
解得:x=25,50-x=25.
答:購進A種計算器25臺,B種計算器25臺.
②設購進A種計算器y臺,則購進C種計算器(50-y)臺,
根據題意得:15y+25(50-y)=900,
解得:y=35,50-y=15.
答:購進A種計算器35臺,B種計算器15臺.
(2)當只購進B、C兩種型號時,
設購進B種計算器z臺,則購進C種計算器(50-z)臺,
根據題意得:21z+25(50-z)=900,
解得:z=$\frac{175}{2}$(不合題意,舍去).
當只購進A、B兩種型號時,
利潤=25×5+25×8=325(元);
當只購進A、C兩種型號時,
利潤=35×5+15×12=421(元).
∵325<421,
∴選擇購進A、C兩種型號的計算器,銷售時獲利最多.
點評 本題考查了一元一次方程的應用,根據數量關系列出一元一次方程(或列式計算)是解題的關鍵.


 新思維假期作業暑假吉林大學出版社系列答案
新思維假期作業暑假吉林大學出版社系列答案科目:初中數學 來源: 題型:選擇題
| A. | 44厘米 | B. | 40厘米 | C. | 36厘米 | D. | 24厘米 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| x(元) | 180 | 260 | 280 | 300 |
| y(間) | 100 | 60 | 50 | 40 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
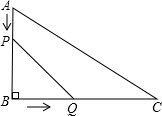 如圖,在△ABC中,∠B=90°,AB=12cm,BC=24cm,動點P從點A開始沿著邊AB向點B以2cm/s的速度移動(不與點B重合),動點Q從點B開始沿著邊BC向點C以4cm/s的速度移動(不與點C重合).若P、Q兩點同時移動t(s);
如圖,在△ABC中,∠B=90°,AB=12cm,BC=24cm,動點P從點A開始沿著邊AB向點B以2cm/s的速度移動(不與點B重合),動點Q從點B開始沿著邊BC向點C以4cm/s的速度移動(不與點C重合).若P、Q兩點同時移動t(s);查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com