試題分析:首先作點M關于AC的對稱點M′,連接M′N交AC于P,此時MP+NP有最小值.然后證明四邊形PMBN為菱形,即可求出MP+NP=BM+BN=BC=5.
作點M關于AC的對稱點M′,連接M′N交AC于P,此時MP+NP有最小值.
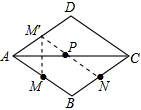
∵菱形ABCD關于AC對稱,M是AB邊上的中點,
∴M′是AD的中點,
又N是BC邊上的中點,
∴AM′∥BN,AM′=BN,
∴四邊形AM′NB是平行四邊形,
∴PN∥AB,
又N是BC邊上的中點,
∴P是AC中點,
∴PM∥BN,PM=BN,
∴四邊形PMBN是平行四邊形,
∵BM=BN,
∴平行四邊形PMBN是菱形.
∴MP+NP=BM+BN=BC=5.
故答案為5.
點評:解答本題的關鍵是判斷當PMBN為菱形時,MP+NP有最小值。





