
 如圖,將長方形紙片ABCD沿其對角線AC折疊,使點B落在點B′的位置,AB′與CD交于點E.
如圖,將長方形紙片ABCD沿其對角線AC折疊,使點B落在點B′的位置,AB′與CD交于點E.分析 (1)由四邊形ABCD為矩形及折疊的特性,得到B′C=BC=AD,∠B′=∠B=∠D=90°,∠B′EC=∠DEA,得到△AED≌△CEB′.
(2))由△AED≌△CEB′,得出EA=EC,所以點E在線段AC的垂直平分線上
(3)陰影部分的周長為AD+DE+EA+EB′+B′C+EC,即矩形的周長;
(4)設B′E=x,則DE=x,CE=CD-x,根據勾股定理即可得到結論.
解答 (1)證明:∵四邊形ABCD為矩形,
∴B′C=BC=AD,∠B′=∠B=∠D=90°
∵∠B′EC=∠DEA,
在△AED和△CEB′中,$\left\{\begin{array}{l}{∠B′ED=∠DEA}\\{∠B′=∠D}\\{B′C=AD}\end{array}\right.$,
∴△AED≌△CEB′(AAS);
(2)∵△AED≌△CEB′,
∴EA=EC,
∴點E在線段AC的垂直平分線上;
(3)∵△AED≌△CEB′,
∴AE=CE,DE=EB′,
∵將長方形紙片ABCD沿其對角線AC折疊,使點B落在點B′的位置,
∴CB′=BC=AD,
∴陰影部分的周長為AD+DE+EA+EB′+B′C+EC,
=AD+DE+EC+EA+EB′+B′C,
=AD+DC+AB′+B′C,
=3+8+8+3
=22;
故答案為:22;
(4)設B′E=x,
則DE=x,CE=CD-x,
∵B′C2+B′E2=CE2,
∴32+x2=(8-x)2,
∴x=$\frac{55}{16}$,
∴EB′=$\frac{55}{16}$.
點評 本題主要考查了圖形的折疊問題,全等三角形的判定和性質,及矩形的性質,勾股定理.熟記翻折前后兩個圖形能夠重合找出相等的角是解題的關鍵.


科目:初中數學 來源: 題型:選擇題
| A. | 6.67×105 | B. | 0.667×107 | C. | 6.67×106 | D. | 66.7×106 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
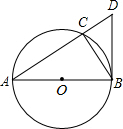 如圖,⊙O是△ABC的外接圓,圓心O在AB上,過點B作⊙O的切線交AC的延長線于點D.
如圖,⊙O是△ABC的外接圓,圓心O在AB上,過點B作⊙O的切線交AC的延長線于點D.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 組別 | 霧霾天氣的主要成因 | 百分比 |
| A | 工業污染 | 45% |
| B | 汽車尾氣排放 | m |
| C | 爐煙氣排放 | 15% |
| D | 其它(濫砍濫伐等) | n |

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
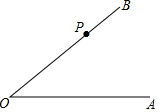 如圖,P是∠AOB的邊OB上一點.
如圖,P是∠AOB的邊OB上一點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com