
分析 將點(-1,-4)代入拋物線解析式中,求出a的值,確定出拋物線解析式即可.
解答 解:(1)∵拋物線y=a(x-h)2+k,當x=1時,y有最值是-2,
∴拋物線y=a(x-1)2-2,
將點(-1,-4)代入y=a(x-1)2-2得:-4=4a-2,
解得:a=-$\frac{1}{2}$,
則拋物線解析式為y=-$\frac{1}{2}$(x-1)2-2.
點評 本題考查了用待定系數法求二次函數解析式的方法.關鍵是根據條件確定拋物線解析式的形式,再求其中的待定系數.一般式:y=ax2+bx+c(a≠0);頂點式y=a(x-h)2+k,其中頂點坐標為(h,k);交點式y=a(x-x1)(x-x2),拋物線與x軸兩交點為(x1,0),(x2,0).


科目:初中數學 來源: 題型:填空題
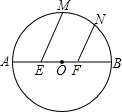 如圖,AB為⊙O的直徑,E、F為AB的三等分點,M、N為$\widehat{AB}$上兩點,且∠MEB=∠NFB=60°,EM+FN=$\sqrt{33}$,則直徑AB的長為6.
如圖,AB為⊙O的直徑,E、F為AB的三等分點,M、N為$\widehat{AB}$上兩點,且∠MEB=∠NFB=60°,EM+FN=$\sqrt{33}$,則直徑AB的長為6.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | -2與$\sqrt{{{(-2)}^2}}$ | B. | -2與$\root{3}{-8}$ | C. | -2與$-\frac{1}{2}$ | D. | 2與|-2| |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com