
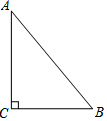
 如圖是一塊直角三角形的綠地,量得直角邊BC為6cm,AC為8cm,現在要將原綠地擴充后成三角形,且擴充的部分是以AC為直角邊的直角三角形,求擴充后的等腰三角形綠地的周長.
如圖是一塊直角三角形的綠地,量得直角邊BC為6cm,AC為8cm,現在要將原綠地擴充后成三角形,且擴充的部分是以AC為直角邊的直角三角形,求擴充后的等腰三角形綠地的周長. 分析 根據題意畫出圖形,構造出等腰三角形,根據等腰三角形及直角三角形的性質利用勾股定理解答.
解答 解:在Rt△ABC中,∠ACB=90°,AC=8m,BC=6m,
由勾股定理有:AB=10m,應分以下三種情況:
①如圖1,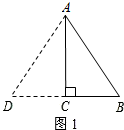
當AB=AD=10m時,
∵AC⊥BD,
∴CD=CB=6m,
∴△ABD的周長=10+10+2×6=32(m).
②如圖2,
當AB=BD=10m時,
∵BC=6m,
∴CD=10-6=4m,
∴AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$(m),
∴△ABD的周長=10+10+4$\sqrt{5}$=(20+4$\sqrt{5}$)m.
③如圖3,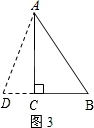
當AB為底時,設AD=BD=x,則CD=x-6,
∵由勾股定理得:AD2=AC2+CD2=82+(x-6)2=x2,
解得x=$\frac{25}{3}$.
∴△ABD的周長為:AD+BD+AB=$\frac{25}{3}$+$\frac{25}{3}$+10=$\frac{80}{3}$(m).
綜上所述,擴充后的等腰三角形綠地的周長為:32m或(20+4$\sqrt{5}$)m或$\frac{80}{3}$m.
點評 本題考查的是勾股定理在實際生活中的運用,在解答此題時要注意分三種情況討論,不要漏解.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,一次函數y=kx+b與反比例函數y=$\frac{6}{x}$(x>0)的圖象交于A(m,6)、B(3,n)兩點
如圖,一次函數y=kx+b與反比例函數y=$\frac{6}{x}$(x>0)的圖象交于A(m,6)、B(3,n)兩點查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 在一次蠟燭燃燒試驗中,甲、乙兩根蠟燭燃燒時剩余部分的高度y(厘米)與燃燒時間x(小時)之間的關系如圖所示,其中乙蠟燭燃燒時y與x之間的函數關系式是y=-10x+25.
在一次蠟燭燃燒試驗中,甲、乙兩根蠟燭燃燒時剩余部分的高度y(厘米)與燃燒時間x(小時)之間的關系如圖所示,其中乙蠟燭燃燒時y與x之間的函數關系式是y=-10x+25.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com