
如圖,在Rt△ABC中,∠ACB=90°,AC=1,BC=7,點(diǎn)D是邊CA延長線的一點(diǎn),AE⊥BD,垂足為點(diǎn)E,AE的延長線交CA的平行線BF于點(diǎn)F,連結(jié)CE交AB于點(diǎn)G.
(1)當(dāng)點(diǎn)E是BD的中點(diǎn)時(shí),求tan∠AFB的值;
(2)CE•AF的值是否隨線段AD長度的改變而變化?如果不變,求出CE•AF的值;如果變化,請說明理由;
(3)當(dāng)△BGE和△BAF相似時(shí),求線段AF的長.


【考點(diǎn)】相似形綜合題;全等三角形的判定與性質(zhì);三角形中位線定理;正方形的判定與性質(zhì);圓的綜合題;銳角三角函數(shù)的定義;特殊角的三角函數(shù)值.
【專題】綜合題.
【分析】(1)過點(diǎn)E作EH⊥CD于H,如圖1,易證EH是△DBC的中位線及△AHE∽△EHD,設(shè)AH=x,運(yùn)用相似三角形的性質(zhì)可求出x,就可求出tan∠AFB的值;
(2)取AB的中點(diǎn)O,連接OC、OE,如圖2,易證四點(diǎn)A、C、B、E共圓,根據(jù)圓周角定理可得∠BCE=∠BAF,根據(jù)圓內(nèi)接四邊形內(nèi)角互補(bǔ)可得∠CBE+∠CAE=180°,由此可推出∠CBE=∠BFA,從而可得△BCE∽△FAB,即可得到CE•FA=BC•AB,只需求出AB就可解決問題;
(3)過點(diǎn)E作EH⊥CD于H,作EM⊥BC于M,如圖3,易證四邊形EMCH是矩形,由△BCE∽△FAB,△BGE與△FAB相似可得△BGE與△BCE相似,即可得到∠EBG=∠ECB.由點(diǎn)A、C、B、E共圓可得∠ECA=∠EBG,即可得到∠ECB=∠ECA,根據(jù)角平分線的性質(zhì)可得EM=EH,即可得到矩形EMCH是正方形,則有CM=CH,易證EB=EA,根據(jù)HL可得Rt△BME∽Rt△AHE,則有BM=AH.設(shè)AH=x,根據(jù)CM=CH可求出x,由此可求出CE的長,再利用(2)中的結(jié)果就可求出AF的值.
【解答】解:(1)過點(diǎn)E作EH⊥CD于H,如圖1,
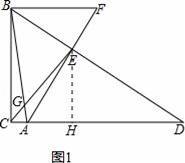

則有∠EHA=∠EHD=90°.
∵∠BCD=90°,BE=DE,
∴CE=DE.
∴CH=DH,
∴EH=
 BC=
BC=
 .
.
設(shè)AH=x,則DH=CH=x+1.
∵AE⊥BD,
∴∠AEH+∠DEH=∠AED=90°.
∵∠AEH+∠EAH=90°,
∴∠EAH=∠DEH,
∴△AHE∽△EHD,
∴
 =
=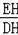
 ,
,
∴EH2=AH•DH,
∴(
 )2=x(x+1),
)2=x(x+1),
解得x=
 (舍負(fù)),
(舍負(fù)),
∴tan∠EAH=
 =
=
 =
=
 .
.
∵BF∥CD,
∴∠AFB=∠EAH,
∴tan∠AFB=
 ;
;
(2)CE•AF的值不變.
取AB的中點(diǎn)O,連接OC、OE,如圖2,
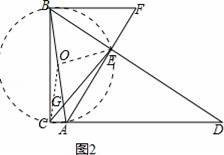

∵∠BCA=∠BEA=90°,
∴OC=OA=OB=OE,
∴點(diǎn)A、C、B、E共圓,
∴∠BCE=∠BAF,∠CBE+∠CAE=180°.
∵BF∥CD,
∴∠BFA+∠CAE=180°,
∴∠CBE=∠BFA,
∴△BCE∽△FAB,
∴
 =
=
 ,
,
∴CE•FA=BC•AB.
∵∠BCA=90°,BC=7,AC=1,
∴AB=5
 ,
,
∴CE•FA=7×5
 =35
=35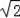
 ;
;
(3)過點(diǎn)E作EH⊥CD于H,作EM⊥BC于M,如圖3,


∴∠EMC=∠MCH=∠CHE=90°,
∴四邊形EMCH是矩形.
∵△BCE∽△FAB,△BGE與△FAB相似,
∴△BGE與△BCE相似,
∴∠EBG=∠ECB.
∵點(diǎn)A、C、B、E共圓,
∴∠ECA=∠EBG,
∴∠ECB=∠ECA,
∴EM=EH,
∴矩形EMCH是正方形,
∴CM=CH.
∵∠ECB=∠ECA=
 ∠BCA=45°,
∠BCA=45°,
∴∠EBA=∠EAB=45°,
∴EB=EA,
∴Rt△BME≌Rt△AHE(HL),
∴BM=AH.
設(shè)AH=x,則BM=x,CM=7﹣x,CH=1+x,
∴7﹣x=1+x,
∴x=3,
∴CH=4.
在Rt△CHE中,
cos∠ECH=
 =
=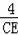
 =
=
 ,
,
∴CE=4
 .
.
由(2)可得CE•FA=35
 ,
,
∴AF=
 =
=
 .
.
【點(diǎn)評】本題主要考查了直角三角形斜邊上的中線等于斜邊的一半、等腰三角形的性質(zhì)、三角形中位線定理、平行線的性質(zhì)、相似三角形的判定與性質(zhì)、全等三角形的判定與性質(zhì)、三角函數(shù)的定義、特殊角的三角函數(shù)值、正方形的判定與性質(zhì)等知識,綜合性強(qiáng),有一定的難度,證到△BCE∽△FAB是解決第(2)小題的關(guān)鍵,證出Rt△BME≌Rt△AHE是解決第(3)小題的關(guān)鍵.


 互動課堂系列答案
互動課堂系列答案 激活思維智能訓(xùn)練課時(shí)導(dǎo)學(xué)練系列答案
激活思維智能訓(xùn)練課時(shí)導(dǎo)學(xué)練系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
如圖,在紙上剪下一個(gè)圓形和一個(gè)扇形的紙片,使之恰好能圍成一個(gè)圓錐模型,若圓的半徑為r,扇形的圓心角等于120°,則圍成的圓錐模型的高為( )


A.r B.2
 r C.
r C.
 r D.3r
r D.3r
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
若將30°、45°、60°的三角函數(shù)值填入表中,則從表中任意取一個(gè)值,是
 的概率為( )
的概率為( )
| α | 30° | 45° | 60° |
| sinα | |||
| cosα | |||
| tanα |
A.
 B.
B.
 C.
C.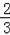
 D.
D.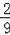

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
甲隊(duì)修路150m與乙隊(duì)修路120m所用天數(shù)相同,已知甲隊(duì)比乙隊(duì)每天多修10m,設(shè)甲隊(duì)每天修路xm.依題意,下面所列方程正確的是( )
A.
 =
=
 B.
B.
 =
=
 C.
C.
 =
=
 D.
D.
 =
=

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
在下列以線段a、b、c的長為三邊的三角形中,不能構(gòu)成直角三角形的是( )
A、a=9,b=41,c=40 B、a=b=5,c=5
C、a∶b∶c=3∶4∶5 D、a=11,b=12,c=15
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com